题目内容
已知椭圆中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆的方程;
(2)设直线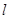 经过点
经过点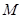 (0,1),且与椭圆交于
(0,1),且与椭圆交于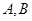 两点,若
两点,若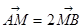 ,求直线
,求直线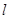 的方程.
的方程.
(1)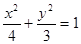 ;(2)
;(2)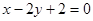 或
或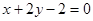 .
.
解析试题分析:本题主要考查椭圆的标准方程和几何性质、直线的方程等基础知识,考查用代数法研究圆锥曲线的性质,考查运算求解能力、综合分析和解决问题的能力.第一问,先利用椭圆的焦距、离心率求出基本量,写出椭圆方程;第二问,由于直线经过(0,1)点,所以先设出直线方程,与椭圆联立,消参得到关于x的方程,先设出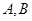 点坐标,通过方程得到两根之和、两根之积,再由
点坐标,通过方程得到两根之和、两根之积,再由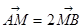 ,得出
,得出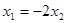 ,联立上述表达式得k的值,从而得到直线方程.
,联立上述表达式得k的值,从而得到直线方程.
试题解析:(1)设椭圆方程为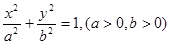 ,
,
因为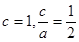 ,所以
,所以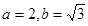 ,
,
所求椭圆方程为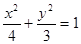 4分
4分
(2)由题得直线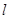 的斜率存在,设直线
的斜率存在,设直线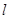 方程为
方程为
则由 得
得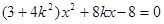 ,
,
设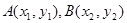 ,则由
,则由 得
得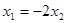 ..8分
..8分
又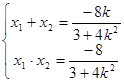 ,
,
所以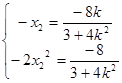 消去
消去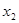 得
得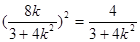
解得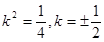
所以直线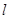 的方程为
的方程为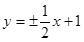 ,即
,即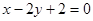 或
或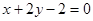 12分
12分
考点:1.椭圆的标准方程;2.直线方程;3.韦达定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
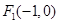 、
、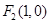 为椭圆
为椭圆 的左、右焦点,且点
的左、右焦点,且点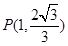 在椭圆
在椭圆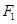 的直线
的直线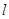 交椭圆
交椭圆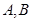 两点,则
两点,则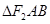 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?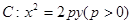 的焦点为
的焦点为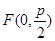 ,准线为
,准线为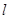 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且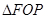 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为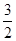 .
.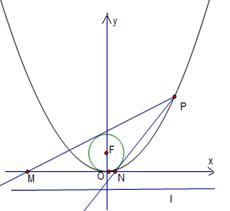
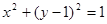 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交 轴于点
轴于点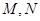 ,求
,求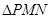 面积的最小值时
面积的最小值时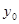 的值.
的值. 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2),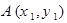 ,
,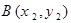 均在抛物线上.
均在抛物线上.
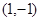 ,求直线AB方程.
,求直线AB方程.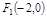 、
、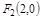 ,动点N满足
,动点N满足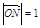 (O为坐标原点),
(O为坐标原点),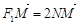 ,
,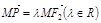 ,
, ,求点P的轨迹方程.
,求点P的轨迹方程.
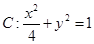 的上、下顶点分别为
的上、下顶点分别为 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点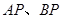 与直线
与直线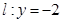 分别交于点
分别交于点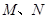 ,
,
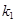 、
、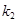 ,求证:
,求证: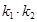 为定值;
为定值;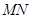 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.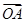 ·
·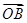 的值;
的值; ,焦点在
,焦点在 轴上的抛物线过点
轴上的抛物线过点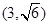 .
.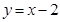 交于
交于 、
、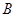 两点,求证:
两点,求证: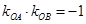 .
.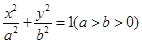 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.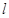 与椭圆相交于不同的两点A,B。已知点A的坐标为
与椭圆相交于不同的两点A,B。已知点A的坐标为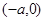 。若
。若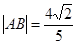 ,求直线
,求直线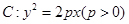 的焦点为
的焦点为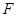 ,准线为
,准线为 ,
,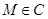 ,以
,以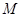 为圆心的圆
为圆心的圆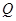 ,
,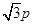 ,
,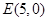 是圆
是圆 轴除
轴除 与圆
与圆 ,
,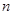 与
与 两点,
两点,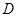 ,且
,且 , 求
, 求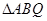 的面积.
的面积.