题目内容
若四边形ABCD满足: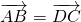 ,且
,且 ,则四边形ABCD的形状是
,则四边形ABCD的形状是
- A.矩形
- B.正方形
- C.等腰梯形
- D.菱形
D
分析:由题意,由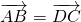 根据向量相等的几何意义可得出,四边形是平行四边形,由
根据向量相等的几何意义可得出,四边形是平行四边形,由 的几何意义得此四边形邻边相等,由这些几何特征即可判断出四边形的确切形状选出正确选项
的几何意义得此四边形邻边相等,由这些几何特征即可判断出四边形的确切形状选出正确选项
解答:由题意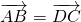 可得出AB
可得出AB CD,由此得,四边形ABCD是平行四边形
CD,由此得,四边形ABCD是平行四边形
又
可得此四边形邻边相等,所以此四边形是菱形
故选D
点评:本题考查向量共线与向量相等的几何意义,由此判断出四边形的形状,解题的关键是熟练掌握向量相等与模相等的意义,由向量关系转化出几何关系,本题数形结合,由代数而几何,题型新颖,是向量考查中常见题型,也是近几年高考试卷上对向量考查的主要形式
分析:由题意,由
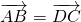 根据向量相等的几何意义可得出,四边形是平行四边形,由
根据向量相等的几何意义可得出,四边形是平行四边形,由 的几何意义得此四边形邻边相等,由这些几何特征即可判断出四边形的确切形状选出正确选项
的几何意义得此四边形邻边相等,由这些几何特征即可判断出四边形的确切形状选出正确选项解答:由题意
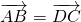 可得出AB
可得出AB CD,由此得,四边形ABCD是平行四边形
CD,由此得,四边形ABCD是平行四边形又

可得此四边形邻边相等,所以此四边形是菱形
故选D
点评:本题考查向量共线与向量相等的几何意义,由此判断出四边形的形状,解题的关键是熟练掌握向量相等与模相等的意义,由向量关系转化出几何关系,本题数形结合,由代数而几何,题型新颖,是向量考查中常见题型,也是近几年高考试卷上对向量考查的主要形式

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
若四边形ABCD满足
=
,则四边形ABCD的形状一定是( )
| AB |
| DC |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |