题目内容
11.已知数列{an}满足a1=2,an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$(n∈N*),则an=$\frac{2}{n}$.分析 由已知求出倒数关系式,从而得到新数列是首项为$\frac{1}{2}$,公差为$\frac{1}{2}$的等差数列,由此能求出a4.
解答 解:∵数列{an}满足:a1=2,an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+$\frac{1}{2}$,
∴{$\frac{1}{{a}_{n}}$}是首项为$\frac{1}{2}$,公差为$\frac{1}{2}$的等差数列,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{2}$+$\frac{1}{2}$(n-1)=$\frac{1}{2}$n,
∴an=$\frac{2}{n}$,
故答案为:$\frac{2}{n}$.
点评 本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.身高不同的7个人排成一排,要求正中间的个子最高,从中间向两边看一个比一个矮,则不同的排法有( )种( )
| A. | 2 | B. | 8 | C. | 20 | D. | 120 |





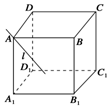 如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.
如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.