题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cosB= .
.
(1)求a,c的值;
(2)求sin(A-B)的值.
[解析] (1)由余弦定理b2=a2+c2-2accosB得,
b2=(a+c)2-2ac(1+cosB),
又已知a+c=6,b=2,cosB= ,∴ac=9.
,∴ac=9.
由a+c=6,ac=9,解得a=3,c=3.
(2)在△ABC中,∵cosB= ,
,
∴sinB= =
= .
.
由正弦定理得sinA= =
= ,
,
∵a=c,∴A为锐角,∴cosA= =
= .
.
∴sin(A-B)=sinAcosB-cosAsinB= .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,
, )的图像如图所示,为了得到函数g(x)=sin2x的图像,则只需将f(x)的图像( )
)的图像如图所示,为了得到函数g(x)=sin2x的图像,则只需将f(x)的图像( )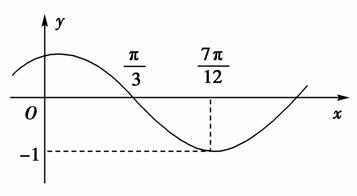
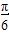 个长度单位
个长度单位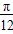 个长度单位
个长度单位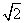 ,则AC=( )
,则AC=( )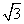 B.2
B.2
 ,B=120°,则a=________
,B=120°,则a=________ km
km km D.10
km D.10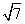 km
km 且z=5y-x的最大值为a,最小值为b,则a-b的值是( )
且z=5y-x的最大值为a,最小值为b,则a-b的值是( )