题目内容
6.若函数y=f(x-1)的定义域为(1,2],则函数y=f(log2x)的定义域为(1,2].分析 由函数y=f(x-1)的定义域为(1,2],得1<x≤2,即0<x-1≤1,则函数y=f(log2x)中,0<log2x≤1,由此能求出函数y=f(log2x)的定义域.
解答 解:由函数y=f(x-1)的定义域为(1,2],
得1<x≤2,
∴0<x-1≤1.
∴函数y=f(log2x)中,0<log2x≤1,
∴1<x≤2.
则函数y=f(log2x)的定义域为(1,2].
故答案为:(1,2].
点评 本题考查对数函数的定义域,解题时要认真审题,仔细解答,注意抽象函数的定义域的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.不论m如何变化,直线(m+2)x-(2m-1)y-(3m-4)=0恒过定点( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
11.已知直线l过点$(\sqrt{3},-2)$和(0,1),则直线l的倾斜角为( )
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
18.集合P={3,log2a},Q={a,b}且P∪Q={0,1,3},则P∩Q等于( )
| A. | {0} | B. | {3} | C. | {0}或{3} | D. | {0,3} |
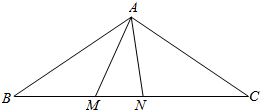 如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上.
如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上. 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{{5\sqrt{3}}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{{5\sqrt{3}}}{2}$.