题目内容
5.在高为H、底面半径为R的圆锥内作一内接圆柱体.则圆柱体的半径r为多大时:(1)圆柱体的体积最大?
(2)圆柱体的表面积最大?
分析 设圆柱底面半径为r,根据三角形相似得出圆柱的高h,代入体积和表面积公式得到关于r的函数,利用导数或基本不等式求出最大值.
解答 解:当圆柱的底面半径为r时,设圆柱体的高为h,
则$\frac{r}{R}=\frac{H-h}{H}$,∴h=$\frac{H(R-r)}{R}$,
(1)圆柱的体积V(r)=πr2h=$\frac{πH(R-r){r}^{2}}{R}$=$\frac{πH(2R-2r)•r•r}{2R}$≤$\frac{πH}{2R}$×($\frac{2R}{3}$)3=$\frac{4πH{R}^{2}}{27}$.当且仅当r=2R-2r即r=$\frac{2R}{3}$时取等号.
(2)圆柱体的表面积S(r)=2πr2+2πrh=2πr2+2πr$\frac{H(R-r)}{R}$=2π(1-$\frac{H}{R}$)r2+2πHr,r∈(0,R).
∴S′(r)=4π$\frac{R-H}{R}$r+2πH,
①当R≥H时,S′(r)>0,故S(r)在(0,R)上是增函数,∴S(r)没有最大值.
②当R<H时,令S′(r)=0,得r=$\frac{HR}{2(H-R)}$,
当0<r<$\frac{HR}{2(H-R)}$时,S′(r)<0,当$\frac{HR}{2(H-R)}$<r<R时,S′(r)>0.
∴当r=$\frac{HR}{2(H-R)}$时,S(r)取得最大值S($\frac{HR}{2(H-R)}$)=$\frac{{H}^{2}Rπ}{2(H-R)}$.
点评 本题考查了圆柱和圆锥的结构特征,体积和表面积计算,导数与函数的最值,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.在△ABC中,∠A,∠B,∠C所对应的边分别为a,b,c,若2∠B=∠A+∠C,且a=1,b=$\sqrt{3}$,则S△ABC=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
17.若tan(π-α)=2,且sinα>0,则cosα=( )
| A. | -$\frac{2\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
15.已知${∫}_{0}^{2}$exdx=e2-1,则${∫}_{0}^{2}$3exdx等于( )
| A. | 6e2-6 | B. | 3e2-3 | C. | ex-1 | D. | e2-1 |
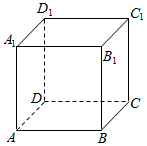 在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小
在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小