题目内容
设函数![]() 为自然对数的底数).
为自然对数的底数).
(1) 若![]() 时,
时, ![]() 恒成立, 求
恒成立, 求![]() 的取值范围;
的取值范围;
(2)求证:对于大于![]() 的正整数
的正整数![]() , 恒有
, 恒有![]() 成立.
成立.
(1) 解: ![]() , ∵
, ∵![]() , ∴
, ∴![]() ,
,![]() .
.
① 若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 为减函数,而
为减函数,而![]() ,
,
从而当![]() 时,
时,![]() ,不合题意,应舍去.
,不合题意,应舍去.
② 若![]() ,则当
,则当![]() 时,
时, ![]() ,
,![]() 为减函数,而
为减函数,而![]() ,
,
从而当![]() 时,
时,![]() ,不合题意,应舍去.
,不合题意,应舍去.
③ 若![]() ,则当
,则当![]() 时,
时, ![]() ,
,![]() 为增函数,而
为增函数,而![]() ,
,
从而当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时, ![]() 恒成立.
恒成立.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
(2)证明: 由(1)知, 对于![]() , 当
, 当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
而当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
从而![]() 时,
时, ![]()
![]() .
.
取![]() ,则
,则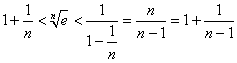 .
.

练习册系列答案
相关题目
 为定义在
为定义在 上的可导函数,且
上的可导函数,且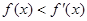 对于
对于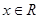 恒成立,设
恒成立,设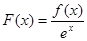 (
(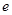 为自然对数的底), 则
为自然对数的底), 则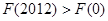 B.
B.
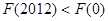
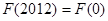 D.
D.
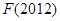 与
与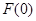 的大小不确定
的大小不确定