题目内容
4.设sinx+siny=$\frac{\sqrt{2}}{2}$,则cosx+cosy的取值范围是( )| A. | [0,$\frac{\sqrt{14}}{2}$] | B. | [-$\frac{\sqrt{14}}{2}$,0] | C. | [-$\frac{\sqrt{14}}{2}$,$\frac{\sqrt{14}}{2}$] | D. | [-$\frac{1}{2}$,$\frac{7}{2}$] |
分析 设cosx+cosy=t,结合已知等式,平方和后利用同角三角函数间的基本关系及两角和与差的余弦函数公式化简,利用余弦函数的值域确定出t的范围即可.
解答 解:设cosx+cosy=t①,sinx+siny=$\frac{\sqrt{2}}{2}$②,
①2+②2得:2+2sinxsiny+2cosxcosy=t2+$\frac{1}{2}$,即cos(x-y)=$\frac{1}{2}$t2-$\frac{3}{4}$,
∵-1≤cos(x-y)≤1,
∴-1≤$\frac{1}{2}$t2-$\frac{3}{4}$≤1,
解得:-$\frac{\sqrt{14}}{2}$≤t≤$\frac{\sqrt{14}}{2}$,
则cosx+cosy的取值范围是:[-$\frac{\sqrt{14}}{2}$,$\frac{\sqrt{14}}{2}$],
故选:C.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
7.函数y=$\sqrt{3}$sin$\frac{1}{2}$x-cos$\frac{1}{2}$x的值域为( )
| A. | [-2,2] | B. | (-2,2) | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | (1,1) |
12.下列各组直线中,互相垂直的一组是( )
| A. | 2x-3y-5=0与4x-6y-5=0 | B. | 2x-3y-5=0与4x+6y+5=0 | ||
| C. | 2x+3y-6=0与3x-2y+6=0 | D. | 2x+3y-6=0与2x-3y-6=0 |
13.在△ABC中,内角A,B,C所对边长分别为a,b,c,若a=$\sqrt{3}$,c-b=1,cos A=$\frac{2}{3}$,则△ABC的面积是$\frac{\sqrt{5}}{2}$.
14.如图所示,表示阴影部分的二元一次不等式组是( )
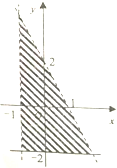

| A. | $\left\{\begin{array}{l}{x+1>0}\\{2x+y<2}\\{y≥-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y≤2}\\{y>-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ |