题目内容
(本小题14分)数列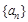 的首项
的首项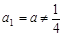 ,且
,且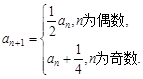
记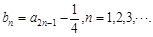
(Ⅰ)求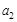 ,
,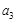 ;
;
(Ⅱ)判断数列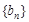 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.
(Ⅲ)求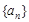 的通项公式.
的通项公式.
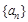 的首项
的首项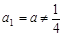 ,且
,且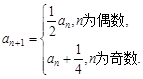
记
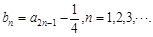
(Ⅰ)求
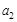 ,
,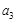 ;
;(Ⅱ)判断数列
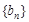 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.(Ⅲ)求
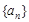 的通项公式.
的通项公式.解:(Ⅰ)
 ,
, ;
;(Ⅱ)因为
 ,所以
,所以 .所以
.所以 ,
, ,
, .猜想,
.猜想, 是公比为
是公比为 的等比数列.证明如下:因为
的等比数列.证明如下:因为 所以
所以 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.(Ⅲ)
 ,
,
略

练习册系列答案
相关题目
题目内容
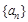 的首项
的首项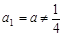 ,且
,且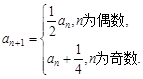
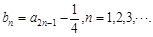
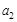 ,
,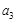 ;
;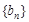 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.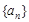 的通项公式.
的通项公式. ,
, ;
; ,所以
,所以 .所以
.所以 ,
, ,
, .猜想,
.猜想, 是公比为
是公比为 的等比数列.证明如下:因为
的等比数列.证明如下:因为 所以
所以 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列. ,
,
