题目内容
已知函数 。
。
(I)若函数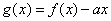 在定义域内为增函数,求实数
在定义域内为增函数,求实数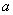 的取值范围;
的取值范围;
(Ⅱ)在(I)的条件下,且 ,
,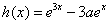 ,
,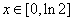 ,求
,求 的极小值;
的极小值;
(Ⅲ) 设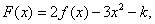
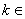
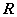 ,若函数
,若函数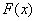 存在两个零点
存在两个零点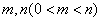 ,且满足
,且满足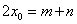 ,问:函数
,问:函数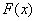 在
在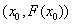 处的切线能否平行于
处的切线能否平行于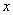 轴?若能,求出该切线方程,若不能,请说明理由。
轴?若能,求出该切线方程,若不能,请说明理由。
解:(Ⅰ)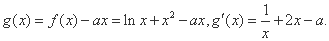
由题意,知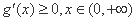 恒成立,即
恒成立,即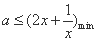 .
.
又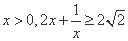 ,当且仅当
,当且仅当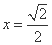 时等号成立.
时等号成立.
故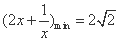 ,所以
,所以 .
.
(Ⅱ)由(Ⅰ)知,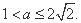 令
令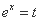 ,则
,则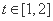 ,则
,则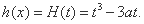
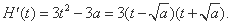
由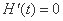 ,得
,得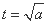 或
或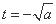 (舍去),
(舍去),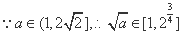 ,
,
①若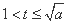 ,则
,则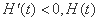 单调递减;
单调递减;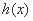 在
在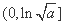 也单调递减;
也单调递减;
②若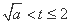 ,则
,则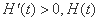 单调递增.
单调递增. 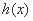 在
在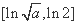 也单调递增;
也单调递增;
故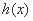 的极小值为
的极小值为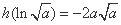
(Ⅲ)设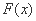 在
在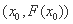 的切线平行于
的切线平行于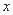 轴,其中
轴,其中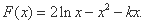 结合题意,
结合题意,
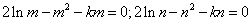 ,相减得
,相减得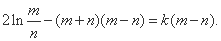
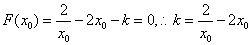 ,又
,又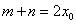 ,
,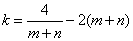
所以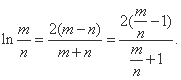 设
设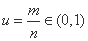 ,
, 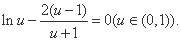
设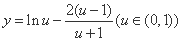 ,
,
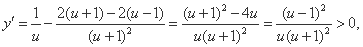
所以函数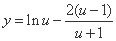 在
在 上单调递增,
上单调递增,
因此,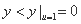 ,即
,即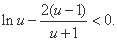
也就是, ,所以
,所以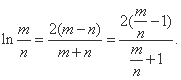 无解。
无解。
所以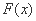 在
在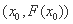 处的切线不能平行于
处的切线不能平行于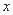 轴。
轴。

练习册系列答案
相关题目
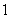 的正方体
的正方体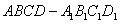 中,点
中,点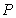 是正方体棱上一点(不包括棱的端点),
是正方体棱上一点(不包括棱的端点),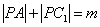 ,
,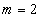 ,则满足条件的点
,则满足条件的点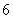 ,则
,则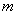 的取值范围是________.
的取值范围是________. 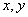 的值如表所示:
的值如表所示: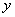
 ,则
,则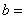 ;
;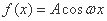 (
(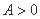 ,
,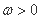 )的部分图像如图所示,其中△
)的部分图像如图所示,其中△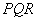 为等腰直角三角形,
为等腰直角三角形, ,
,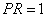 。
。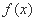 的解析式;
的解析式;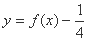 在
在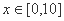 时的所有零点之和。
时的所有零点之和。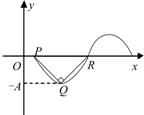
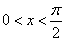 ,则
,则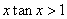 是
是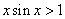 的
的 
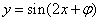 的图象沿
的图象沿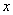 轴向左平移
轴向左平移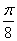 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则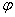 的一个可能取值为( )
的一个可能取值为( ) B.
B. C.
C.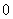 D.
D.