题目内容
若tanθ=2，求下列各式的值．
（1）
；
（2）3sin2θ-2sinθcosθ-1．
（1）
| 3sinθ-2cosθ |
| 2sinθ+cosθ |
（2）3sin2θ-2sinθcosθ-1．
（1）原式=
，
把tanθ=2代入，
得原式=
=
.
（2）3sin2θ-2sinθcosθ-1
=3sin2θ-2sinθcosθ-sin2θ-cos2θ
=2sin2θ-2sinθcosθ-cos2θ
=cos2θ（2tan2θ-2tanθ-1）
∵tanθ=2
∴
=2得cos2θ=
，
则原式=
(2•22-2•2-1)=
.
| 3tanθ-2 |
| 2tanθ+1 |
把tanθ=2代入，
得原式=
| 3sinθ-2cosθ |
| 2sinθ+cosθ |
| 4 |
| 5 |
（2）3sin2θ-2sinθcosθ-1
=3sin2θ-2sinθcosθ-sin2θ-cos2θ
=2sin2θ-2sinθcosθ-cos2θ
=cos2θ（2tan2θ-2tanθ-1）
∵tanθ=2
∴
| sinθ |
| cosθ |
| 1 |
| 5 |
则原式=
| 1 |
| 5 |
| 3 |
| 5 |
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，正方形ABCD的边长为4，E为CD的中点，F为AD边上一点，且不与点D重合，AF=a，
tan
=
cos
=2cos
cos
tan
=
cos
=2cos
cos
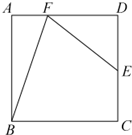如图，正方形ABCD的边长为4，E为CD的中点，F为AD边上一点，且不与点D重合，AF=a，