题目内容
已知定义在区间[-π,
]上的函数y=f(x)的图象关于直线x=-
对称,当x≤-
时,f(x)=sinx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
A、-
| ||
| B、-π | ||
C、-
| ||
D、-
|
分析:(Ⅲ)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案
解答:解:作函数f(x)的图象(如图),
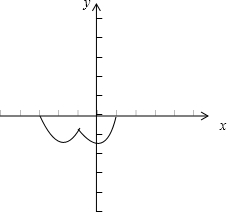
显然,若f(x)=a有解,则a∈[-1,0]
①-1<a<-
,f(x)=a有4解,S=-π②
a=-
,f(x)=a有三解,S=-
π
③-
<a<0或a=-1,f(x)=a有2解,S=-
故选A.

显然,若f(x)=a有解,则a∈[-1,0]
①-1<a<-
| ||
| 2 |
a=-
| ||
| 2 |
| 3 |
| 4 |
③-
| ||
| 2 |
| π |
| 2 |
故选A.
点评:本题考查的知识点是函数解析式的求法--图象变换法,根的存在性及根的个数的判断,其中根据 y=f(x)的图象关于直线x=-
对称,当x≤-
时,函数f(x)=sinx.根据对称变换法则,求出函数的解析式是解答本题的关键.
| π |
| 4 |
| π |
| 4 |

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
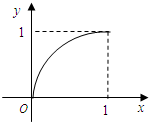 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: