题目内容
已知a为常数,f(x)=lg(| a | 1+x |
(1)求a的值,并求出f(x)的定义域;
(2)解不等式f(x)>-1.
分析:(1)根据奇函数的定义可得 f(-x)+f(x)=0,故f0)=0,故lg(a-1)=0,解得a的值.
(2)f(x)=lg
,不等式f(x)>-1即 lg
≥lg
,即
≥
,移项后,用穿根法求得解集,最后得函数的定义域求出交集即可.
(2)f(x)=lg
| 1-x |
| 1+x |
| 1-x |
| 1+x |
| 1 |
| 10 |
| 1-x |
| 1+x |
| 1 |
| 10 |
解答:解:(1)根据奇函数的定义可得 f(-x)+f(x)=0,
∴故f0)=0,故lg(a-1)=0,a-1=1,故a=2.
(2)由以上可得 f(x)=lg
,
由
可得-1<x<1,故f(x)的定义域为(-1,1).
不等式f(x)>-1即 lg
>lg
,
即
>
,
移项后,得:
<0,
用穿根法求得-1<x<
.
综上,不等式的解集为(-1,
).
∴故f0)=0,故lg(a-1)=0,a-1=1,故a=2.
(2)由以上可得 f(x)=lg
| 1-x |
| 1+x |
由
|
不等式f(x)>-1即 lg
| 1-x |
| 1+x |
| 1 |
| 10 |
即
| 1-x |
| 1+x |
| 1 |
| 10 |
移项后,得:
x-
| ||
| 1+x |
用穿根法求得-1<x<
| 9 |
| 11 |
综上,不等式的解集为(-1,
| 9 |
| 11 |
点评:本题考查对数函数的定义域,奇函数的定义,对数函数的单调性和特殊点,体现了转化的数学思想,解不等式lg
≥-1,是解题的难点.
| 1+x |
| 1-x |

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
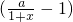 是奇函数.
是奇函数.