题目内容
20.计算:(1)$\frac{{m+{m^{-1}}+2}}{{{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}}}$
(2)$\frac{lg8+lg125-lg2-lg5}{lg\sqrt{10}lg0.1}$.
分析 (1)利用平方和公式化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)$\frac{{m+{m^{-1}}+2}}{{{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}}}=\frac{{{{({{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}})}^2}}}{{{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}}}={m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}$-----------------(5分)
(2)$\frac{lg8+lg125-lg2-lg5}{lg\sqrt{10}lg0.1}$=-----------------------------(2分)
=$\frac{{3({lg2+lg5})-(lg2+lg5)}}{{\frac{1}{2}lg10•lg{{10}^{-1}}}}=\frac{2}{{-\frac{1}{2}}}=-4$---------------------------(5分)
点评 本题考查有理指数幂以及对数运算法则的化简求解,考查计算能力.

练习册系列答案
相关题目
10.已知函数f(x)=$\sqrt{x+3}$+$\frac{1}{x+2}$,则f(-3)=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.下列函数中,既是奇函数又存在零点的是( )
| A. | y=cosx | B. | y=sinx | C. | y=lnx | D. | y=$\frac{1}{x}$ |
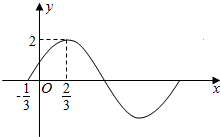 己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.