题目内容
已知在四棱锥 中,底面
中,底面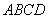 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱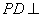 平面
平面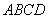 ,且
,且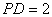 ,
, 为底面对角线的交点,
为底面对角线的交点,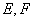 分别为棱
分别为棱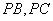 的中点
的中点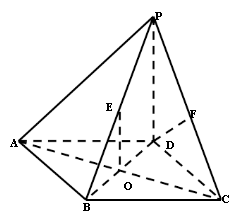
(1)求证: //平面
//平面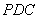 ;
;
(2)求证: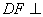 平面
平面 ;
;
(3)求点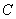 到平面
到平面 的距离。
的距离。
(1)证明: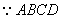 是正方形,,
是正方形,, 为
为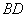 的中点,又
的中点,又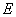 为
为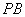 的中点,
的中点,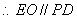 ,且
,且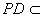 平面
平面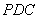 ,
,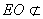 平面
平面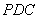 ,
,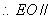 平面
平面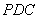 . 4分
. 4分
(2)证明: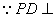 面
面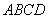 ,
,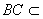 面
面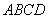 ,
,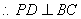 ,又可知
,又可知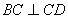 ,而
,而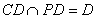 ,
,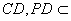 面
面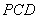 ,
,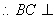 面
面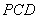 ,
,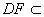 面
面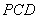 ,
,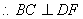 ,又
,又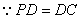 ,
,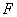 为
为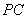 的中点,
的中点,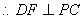 ,而
,而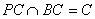 ,
,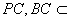 平面
平面 ,
,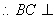 平面
平面 ;
;
(3)点 到平面
到平面 的距离为
的距离为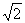 .
.
解析试题分析:(1)证明: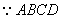 是正方形,,
是正方形,,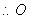 为
为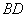 的中点,又
的中点,又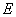 为
为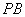 的中点,
的中点,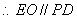 ,且
,且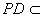 平面
平面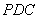 ,
,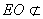 平面
平面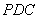 ,
,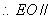 平面
平面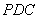 . 4分
. 4分
(2)证明: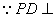 面
面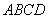 ,
,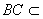 面
面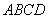 ,
,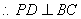 ,又可知
,又可知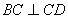 ,而
,而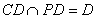 ,
,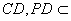 面
面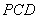 ,
,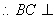 面
面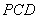 ,
,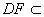 面
面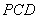 ,
,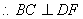 ,又
,又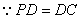 ,
,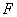 为
为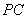 的中点,
的中点,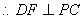 ,而
,而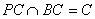 ,
,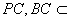 平面
平面 ,
,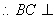 平面
平面 8分
8分
(3)解:设点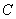 到平面
到平面 的距离为
的距离为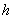 ,由(2)易证
,由(2)易证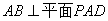 ,
,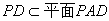 ,
,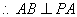 ,
,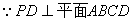 ,
,
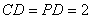
又 ,即
,即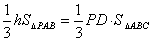 ,
,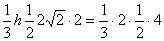 ,得
,得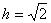
即点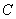 到平面
到平面 的距离为
的距离为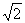 12分
12分
考点:本题主要考查立体几何中的平行关系、垂直关系,距离的计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。要注意将立体几何问题转化成了平面几何问题。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 中,
中,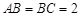 ,过
,过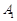 、
、 、
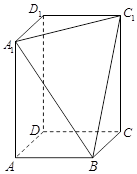
、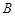 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体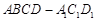 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
 的长;
的长; 到平面
到平面 的距离.
的距离. 平面EFDC.
平面EFDC.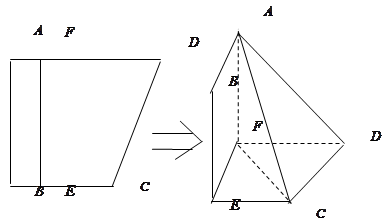
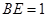 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点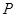 ,且
,且 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出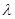 的值;若不存在,说明理由;
的值;若不存在,说明理由;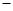 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.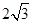 EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
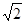 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.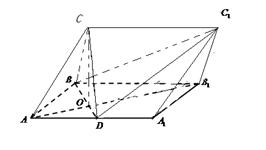
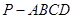 中,底面
中,底面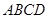 是矩形,
是矩形,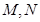 分别为
分别为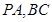 的中点,
的中点,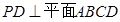 ,且
,且
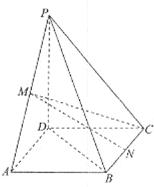
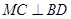 ;
; 的余弦值。
的余弦值。 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,
所在平面互相垂直,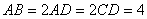 ,
,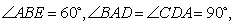 点
点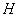 ,
,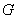 分别是线段
分别是线段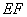 ,
, 的中点.
的中点. 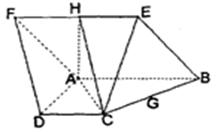
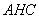
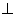 平面
平面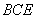 ;
;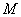 在直线
在直线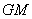 //平面
//平面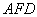 ,求平面
,求平面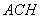 与平面
与平面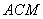 所成角的余弦值。
所成角的余弦值。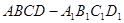 中,面
中,面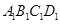 中心为
中心为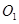 .
.
 面
面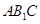 ;
;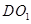 与
与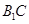 所成角.
所成角.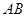 为圆
为圆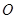 的直径,点
的直径,点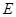 、
、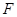 在圆
在圆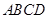 所在的平面和圆
所在的平面和圆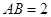 ,
,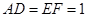 .
.
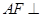 平面
平面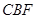 ;
;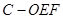 的体积.
的体积.