题目内容
如图,在三棱锥 中,
中, 是等边三角形,
是等边三角形, .
.

(1)证明:: ;
;
(2)证明: ;
;
(3)若 ,且平面
,且平面 平面
平面 ,求三棱锥
,求三棱锥 体积.
体积.
 中,
中, 是等边三角形,
是等边三角形, .
.
(1)证明::
 ;
;(2)证明:
 ;
;(3)若
 ,且平面
,且平面 平面
平面 ,求三棱锥
,求三棱锥 体积.
体积.(1)详见解析;(2)详见解析;(3) .
.
 .
.试题分析:(1)先证明
 ,从而得到
,从而得到 ;(2)取
;(2)取 的中点
的中点 ,连接
,连接 、
、 ,证明
,证明 平面
平面 ,利用直线与平面垂直的性质得到
,利用直线与平面垂直的性质得到 ;(3)作
;(3)作 ,垂足为
,垂足为 ,连结
,连结 ,结合(2)中的结论证明
,结合(2)中的结论证明 平面
平面 ,再求出
,再求出 的面积,最后利用分割法得到三棱锥
的面积,最后利用分割法得到三棱锥 的体积
的体积 来进行计算.
来进行计算.试题解析:(1)因为
 是等边三角形,
是等边三角形, ,
,所以
 ,可得
,可得 ;
;(2)如图,取
 中点
中点 ,连结
,连结 、
、 ,则
,则 ,
, ,
,所以
 平面
平面 ,所以
,所以 ;
;
(3)作
 ,垂足为
,垂足为 ,连结
,连结 ,
,因为
 ,所以
,所以 ,
, ,
,由已知,平面
 平面
平面 ,故
,故 ,
,因为
 ,所以
,所以 、
、 、
、 都是等腰直角三角形.
都是等腰直角三角形.由已知
 ,得
,得 ,
, 的面积
的面积 ,
,因为
 平面
平面 ,
,所以三棱锥
 的体积
的体积 .
.
练习册系列答案
相关题目
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱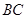 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示); 平面ABC,
平面ABC, ,
,

 ,
, 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数 的正方体
的正方体 中,点
中,点 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且满足
上,且满足 .
.
 ;
; 上确定一点
上确定一点 ,使
,使 、
、 的长;
的长; 的体积.
的体积. 中侧棱垂直于底面,
中侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱 中,
中,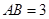 ,
, ,
, ,若把
,若把 旋转一周,则所形成的几何体的体积是( )
旋转一周,则所形成的几何体的体积是( )




 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.