题目内容
已知全集U=R,A={x|-
x2+x+1>0},B={x|3x2-4x+1>0},求∁U(A∩B).
| 3 |
| 4 |
考点:交、并、补集的混合运算
专题:集合
分析:求出A与B中不等式的解集确定出A与B,找出A与B交集的补集即可.
解答:
解:由A中不等式变形得:3x2-4x-4<0,即(x-2)(3x+2)<0,
解得:-
<x<2,即A={x|-
<x<2},
由B中不等式变形得:(3x-1)(x-1)>0,
解得:x<
或x>1,即B={x|x<
或x>1},
∴A∩B={x|-
<x<
或1<x<2},
则∁U(A∩B)={x|x≤-
或
≤x≤1或x≥2}.
解得:-
| 2 |
| 3 |
| 2 |
| 3 |
由B中不等式变形得:(3x-1)(x-1)>0,
解得:x<
| 1 |
| 3 |
| 1 |
| 3 |
∴A∩B={x|-
| 2 |
| 3 |
| 1 |
| 3 |
则∁U(A∩B)={x|x≤-
| 2 |
| 3 |
| 1 |
| 3 |
点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
函数f(x)=ax-2(a>0且a≠1)的图象过定点( )
| A、(0,1) |
| B、(1,0) |
| C、(2,0) |
| D、(2,1) |
设a=sin(-810°),b=tan(
),c=lg
,则它们的大小关系为( )
| 33π |
| 8 |
| 1 |
| 5 |
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、c<a<b |
已知θ是第一象限角,则方程x2+y2sinθ=1表示的图形是( )
| A、圆 | B、椭圆 |
| C、双曲线 | D、圆或椭圆 |
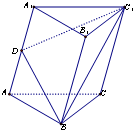 如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )
如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )| A、2:3 | B、1:1 |
| C、3:2 | D、3:4 |