题目内容
5.袋中有1--4号4个均匀的球,从中取出一个放回再取,设第一次所取球号数与第二次所取球号数商为X,求X的分布列.分析 从袋中取出一个放回再取一球,用列举法求出基本事件数;
从而得出第一次所取球号数与第二次所取球号数的商可能取值X,计算对应的概率即可.
解答 解:根据题意,从袋中取出一个放回再取一球,有
11,12,13,14,21,22,23,24,31,32,33,34,41,42,43,44共16种;
设第一次所取球号数与第二次所取球号数商为X,
则X的可能取值为$\frac{1}{4}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{1}{2}$,$\frac{3}{4}$,1,$\frac{3}{2}$,$\frac{4}{3}$,2,3,4;
∴P($\frac{1}{4}$)=$\frac{1}{16}$,
P($\frac{1}{3}$)=$\frac{1}{16}$,
P($\frac{1}{2}$)=$\frac{1}{8}$,
P($\frac{2}{3}$)=$\frac{1}{16}$,
P($\frac{3}{4}$)=$\frac{1}{16}$,
P(1)=$\frac{1}{4}$,
P($\frac{3}{2}$)=$\frac{1}{16}$,
P($\frac{4}{3}$)=$\frac{1}{16}$,
P(2)=$\frac{1}{8}$,
P(3)=$\frac{1}{16}$,
P(4)=$\frac{1}{16}$;
∴X的分布列为
| X | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | 1 | $\frac{3}{2}$ | $\frac{4}{3}$ | 2 | 3 | 4 |
| P | $\frac{1}{16}$ | $\frac{1}{16}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{16}$ | $\frac{1}{4}$ | $\frac{1}{16}$ | $\frac{1}{16}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{16}$ |
点评 本题考查了用列举法计算基本事件的概率以及离散型随机事件的分布列的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知函数f(x)为R上的奇函数,且当x≥0时,f(x)=3x-a,则f(-2)=( )
| A. | -10 | B. | -8 | C. | 10 | D. | 8 |
20.sin113°cos22°+sin203°sin158°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
10.若函数f(x)=$\frac{sinx}{x}$,并且$\frac{π}{3}$<a<b<$\frac{2π}{3}$,则下列各结论中正确的是( )
| A. | f(a)<f($\sqrt{ab}$)<f($\frac{a+b}{2}$) | B. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(b) | C. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(a) | D. | f(b)<f($\frac{a+b}{2}$)<f($\sqrt{ab}$) |
17.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 4 | B. | 21+$\sqrt{3}$ | C. | 3$\sqrt{3}$+12 | D. | $\frac{{3\sqrt{3}}}{2}$+12 |
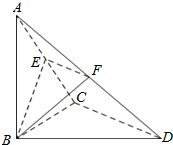 如图5,已知△BCD中,∠BCD=90°,BC=CD=1,AB=$\sqrt{6}$,AB⊥平面BCD,E、F分别是AC、AD的中点.
如图5,已知△BCD中,∠BCD=90°,BC=CD=1,AB=$\sqrt{6}$,AB⊥平面BCD,E、F分别是AC、AD的中点.