题目内容
3.对任意实数b及非零实数a,不等式|2a+b|+|a-b|≥|a|(|2x-1|-|x-2|)恒成立,试求x的取值范围.分析 把原不等式变形,得$\frac{{|{2a+b}|+|{a-b}|}}{a}≥|{2x-1}|-|{x-2}|$,求出左边的最小值,转化为|2x-1|-|x-2|≤3,分类求解得答案.
解答 解:∵a≠0,∴原不等式等价于$\frac{{|{2a+b}|+|{a-b}|}}{a}≥|{2x-1}|-|{x-2}|$,
∵|2a+b|+|a-b|≥|(2a+b)+(a-b)|,当且仅当(2a+b)(a-b)≥0时取等号,
∴$\frac{|2a+b|+|a-b|}{|a|}≥3$,即$\frac{|2a+b|+|a-b|}{|a|}$的最小值是3.
依题应有|2x-1|-|x-2|≤3.
下面解不等式|2x-1|-|x-2|≤3,它等价于
$\left\{\begin{array}{l}{x≥2}\\{(2x-1)-(x-2)≤3}\end{array}\right.$,①
或$\left\{\begin{array}{l}{\frac{1}{2}≤x<2}\\{(2x-1)+(x-2)≤3}\end{array}\right.$,②
或$\left\{\begin{array}{l}{x<\frac{1}{2}}\\{1-2x+(x-2)≤3}\end{array}\right.$,③
解①得x=2; 解②得$\frac{1}{2}≤x<2$; 解③得-4$≤x<\frac{1}{2}$.
综上所述知,x的取值范围是[-4,2].
点评 本题考查绝对值不等式的解法,考查了数学转化思想方法,训练了恒成立问题的求解方法,是中档题.

练习册系列答案
相关题目
13.执行如图所示的程序框图,若输出的结果为2,则可输入的实数x值的个数为( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.已知i是虚数单位,则复数z=$\frac{4+3i}{3-4i}$的共轭复数的虚部是( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
18.下列说法正确的是( )
| A. | 命题:?x∈R,使得ex>0的否定是:?x∈R,有ex>0 | |
| B. | 命题:已知x,y∈R,若x+y≠4,则x≠2或y≠2是真命题 | |
| C. | 不等式f(x)≥g(x)恒成立?f(x)min≥g(x)max | |
| D. | 命题:若a=-1,则函数f(x)=ax2+2x-1只有一个零点的否命题为真命题 |
15.已知数列{an}的前n项和S${\;}_{n}=A{q}^{n}+B(q≠0)$,则“A=-B“是“数列{an}是等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
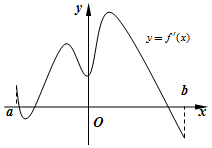 函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.
函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.