题目内容
12.求函数y=-3sin2x+9sinx+$\frac{5}{4}$的最大值.分析 令sinx=t,则t∈[-1,1],换元并配方可得y=-3(t-$\frac{3}{2}$)2+8,由二次函数区间的最值可得.
解答 解:令sinx=t,则t∈[-1,1],
换元可得y=-3t2+9t+$\frac{5}{4}$
=-3(t2-3t+$\frac{9}{4}$)+8
=-3(t-$\frac{3}{2}$)2+8,
由二次函数可知当t=1时,
函数取最大值$\frac{29}{4}$
点评 本题考查三角函数的最值,换元后利用二次函数区间的最值是解决问题的关键,属基础题.

练习册系列答案
相关题目
2.若x>0,且x≠1,则函数y=lgx+logx10的值域为( )
| A. | R | B. | [2,+∞) | C. | (-∞,-2] | D. | (-∞,-2]∪[2,+∞) |
1.设函数f(x)=$\frac{{x}^{2}-x+2}{{x}^{2}}$,若对x>0恒有xf(x)+a>0成立,则实数a的取值范围是( )
| A. | (-∞,1-2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$-1) | C. | (2$\sqrt{2}$-1,+∞) | D. | (1-2$\sqrt{2}$,+∞) |
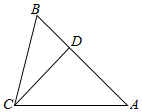 △ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.
△ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC. 某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.