题目内容
已知tan(α+
解析:∵tan(α+![]() )=1+
)=1+![]() =2,
=2,
∴tanα=![]() .
.
于是cos2α+3sin2α+tan2α
=cos2α-sin2α+3sin2α+![]()
=cos2α+2sin2α+![]() =
=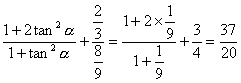 .
.
答案:![]()

练习册系列答案
相关题目
已知tan(θ+
)=-3,则sin2θ+sinθcosθ-2cos2θ=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
题目内容
已知tan(α+
解析:∵tan(α+![]() )=1+
)=1+![]() =2,
=2,
∴tanα=![]() .
.
于是cos2α+3sin2α+tan2α
=cos2α-sin2α+3sin2α+![]()
=cos2α+2sin2α+![]() =
=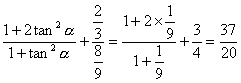 .
.
答案:![]()

| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|