题目内容
已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,求动圆圆心M的轨迹方程.
M的轨迹方程是 =1(x≥
=1(x≥ )
)
 =1(x≥
=1(x≥ )
)设动圆M的半径为r,

则由已知|MC1|=r+ ,
,
|MC2|=r- ,
,
∴|MC1|-|MC2|=2 .
.
又C1(-4,0),C2(4,0),
∴|C1C2|=8,∴2 <|C1C2|.
<|C1C2|.
根据双曲线定义知,点M的轨迹是以C1(-4,0)、C2(4,0)为焦点的双曲线的右支.
∵a= ,c=4,
,c=4,
∴b2=c2-a2=14,
∴点M的轨迹方程是 =1(x≥
=1(x≥ ).
).

则由已知|MC1|=r+
 ,
,|MC2|=r-
 ,
,∴|MC1|-|MC2|=2
 .
.又C1(-4,0),C2(4,0),
∴|C1C2|=8,∴2
 <|C1C2|.
<|C1C2|.根据双曲线定义知,点M的轨迹是以C1(-4,0)、C2(4,0)为焦点的双曲线的右支.
∵a=
 ,c=4,
,c=4,∴b2=c2-a2=14,
∴点M的轨迹方程是
 =1(x≥
=1(x≥ ).
).
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
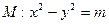 ,
,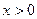 ,
,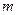 为正常数.直线
为正常数.直线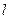 与曲线
与曲线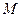 的实轴不垂直,且依次交直线
的实轴不垂直,且依次交直线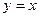 、曲线
、曲线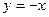 于
于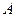 、
、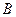 、
、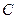 、
、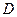 4个点,
4个点,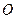 为坐标原点.
为坐标原点.
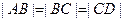 ,求证:
,求证: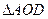 的面积为定值;
的面积为定值;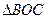 的面积等于
的面积等于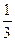 ,求证:
,求证: ,则a+b的值为( )
,则a+b的值为( )
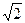 +1
+1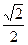 +1
+1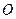 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为 ,离心率
,离心率 .
. 的坐标为
的坐标为 ,
,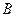 是圆
是圆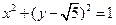 上的点,点
上的点,点 在双曲线右支上,求
在双曲线右支上,求 的最小值,并求此时
的最小值,并求此时
 的渐近线与抛物线
的渐近线与抛物线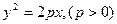 交于三个不同的点O,A,B,(其中0是坐标原点),若
交于三个不同的点O,A,B,(其中0是坐标原点),若 为等边三角形,则双曲线的离心率为
为等边三角形,则双曲线的离心率为 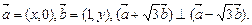
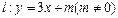 与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.
与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.