题目内容
已知抛物线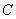 :
: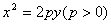 的准线为
的准线为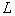 ,焦点为
,焦点为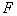 ,
,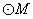 的圆心在
的圆心在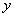 轴的正半轴上,且与
轴的正半轴上,且与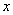 轴相切,过原点作倾斜角为
轴相切,过原点作倾斜角为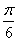 的直线
的直线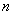 ,交
,交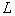 于点
于点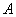 ,交
,交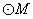 于另一点
于另一点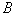 ,且
,且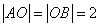
(I) 求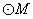 和抛物线
和抛物线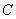 的方程;
的方程;
(II) 过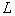 上的动点
上的动点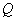 作
作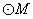 的切线,切点为
的切线,切点为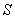 、
、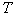 ,求当坐标原点
,求当坐标原点 到直线
到直线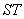 的距离取得最大值时,四边形
的距离取得最大值时,四边形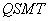 的面积.
的面积.
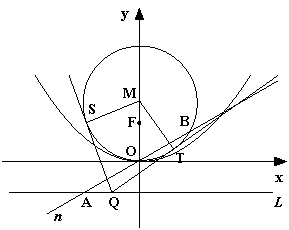 |
(1)准线L交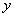 轴于
轴于 ,在
,在 中
中 所以
所以 ,所以
,所以 ,抛物线方程是
,抛物线方程是 (3分)
(3分)
在 中有
中有 ,所以
,所以
所以⊙M方程是:  (6分)
(6分)
(2)解法一 设
所以:切线 ;切线
;切线 (8分)
(8分)
因为SQ和TQ交于Q点所以
 和
和 成立
成立
所以ST方程: (10分)
(10分)
所以原点到ST距离 ,当
,当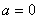 即Q在y轴上时d有最大值
即Q在y轴上时d有最大值
此时直线ST方程是 (11分)
(11分)
所以
所以此时四边形QSMT的面积 (12分)
(12分)
说明:此题第二问解法不唯一,可酌情赋分.
只猜出“直线ST方程是 ”未说明理由的, 该问给2分
”未说明理由的, 该问给2分
利用SMTQ四点共圆的性质,写出以QM为直径的圆方程 得2分
两圆方程相减得到直线ST方程 得4分
以后步骤赋分参照解法一.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ,若数列
,若数列 满足
满足 ,
,
 、
、 的距离之和是4,且曲
的距离之和是4,且曲 的面积的最小值为
的面积的最小值为 C. 8 D. 2
C. 8 D. 2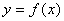 的图象与直线
的图象与直线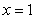 的交点个数为0或1;
的交点个数为0或1;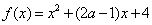 , 若当
, 若当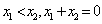 时,总有
时,总有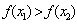 ,
,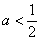 ;
;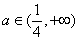 时,函数
时,函数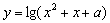 的值域为
的值域为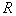 ;
;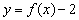 的图象关于点
的图象关于点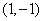 对称的图象对应的函数为
对称的图象对应的函数为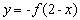 .
. ;②
;② ;③
;③ ;④
;④ . 则输出函数的序号为
. 则输出函数的序号为
 其中
其中 ,则
,则 有
有 内的三个根
内的三个根 内的四个根
内的四个根 内的三个根
内的三个根 的离心率为
的离心率为 ,且抛物线
,且抛物线 的焦点为
的焦点为 ,点
,点 在此抛物线上,
在此抛物线上, 为线段
为线段 的中点,则点
的中点,则点 B、
B、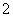 C、
C、 D、
D、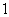
 与
与 之间的距离为
之间的距离为  B.
B. C. 1 D.
C. 1 D. 