题目内容
求下列函数的值域：
（1）y=|x-2|；
（2）y=|x2+1|；
（3）y=|x+2|+|2x+3|．
（1）y=|x-2|；
（2）y=|x2+1|；
（3）y=|x+2|+|2x+3|．
考点：函数的值域
专题：计算题,函数的性质及应用
分析：绝对值函数求值域，分类讨论后求取值范围．
解答：
解：（1）y=|x-2|≥0；
则函数y=|x-2|的值域为[0，+∞）．
（2）|x2+1|≥1；
则函数y=|x2+1|的值域为[1，+∞）．
（3）y=|x+2|+|2x+3|=
；
则y≥
．
则函数y=|x+2|+|2x+3|的值域为[
，+∞）．
则函数y=|x-2|的值域为[0，+∞）．
（2）|x2+1|≥1；
则函数y=|x2+1|的值域为[1，+∞）．
（3）y=|x+2|+|2x+3|=
|
则y≥
| 1 |
| 2 |
则函数y=|x+2|+|2x+3|的值域为[
| 1 |
| 2 |
点评：绝对值函数求值域，分类讨论后求取值范围．是基础题．
练习册系列答案
相关题目
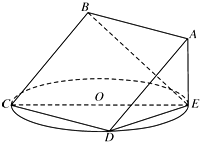如图，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点．