题目内容
3．已知函数y=f（x）的图象在点（2，f（2））处的切线方程为x+2y+1=0，则f（2）-2f′（2）的值为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | -1 | D． | $-\frac{1}{2}$ |
分析 先将x=2代入切线方程可求出f（2），再由切点处的导数为切线斜率可求出f'（2）的值，最后代入即可．
解答 解：由已知切点在切线上，
所以f（2）=-$\frac{3}{2}$，
切点处的导数为切线斜率，
所以f'（2）=-$\frac{1}{2}$，
所以f（2）-2f′（2）=-$\frac{3}{2}$+1=-$\frac{1}{2}$．
故选D．
点评 本题主要考查导数的几何意义，即函数在某点的导数值等于以该点为切点的切线的斜率．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
16．函数y=sin（2x+φ），φ∈（0，2π）的部分图象如图所示，则φ的值为（ ）
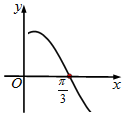
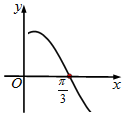
| A． | $\frac{π}{3}$ | B． | $\frac{4π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{π}{3}$或$\frac{4π}{3}$ |
14．已知复数z满足（1+3i）z=10，则z=（ ）
| A． | -1-3i | B． | 1+3i | C． | -1+3i | D． | 1-3i |
11．已知奇函数y=f（x）满足：f（x）=f（x+2），且当x∈（0，1）时，f（x）=2x-1，则f（-4.5）=（ ）
| A． | -2 | B． | -1 | C． | $-\frac{1}{2}$ | D． | 0 |