Question

已知双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的离心率e=

5

2

，虚轴的下端点为B，过双曲线的右焦点F（c，0）作垂直于x轴的直线交双曲线与P，若点A满足：2

OA

=

OF

+

OP

（O为坐标原点），且

OA

•

OB

=-

1

4

（1）求双曲线的方程；
（2）过点C（0，-2）的直线l交该双曲线与不同两点M，N，求

OM

•

ON

的取值范围．

Answer 1

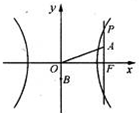
分析：（1）由已知，点B，F，P的坐标分别为B（0，-b），F（c，0），P（c，

b2

a

），由2

OA

=

OF

+

OP

，知点A的坐标为(c，

b2

2a

)，

OA

=(c，

b2

2a

)，

OB

=(0，-b)，由

OA

•

OB

=-

1

4

，知a=2b³．由此能求出双曲线方程．
（2）设直线l的方程为y=kx-2，联立方程组

x2 4 -y2=1 y=kx-2

，得（1-4k²）x²+16kx-20=0，设M（x₁，y₁），N（x₂，y₂），由

1-4 k2≠0 △=(16k )2+80(1-4k2)＞0

，解得k2＜

5

4

，且k2≠

1

4

，x1+x2=

16k

4k2-1

，x1x2=

20

4k2-1

，所以

OM

•

ON

=x1x2+y1y2=1+

17

4k2-1

，由此能求出

OM

•

ON

的范围．

解答：解：（1）由已知，点B，F，P的坐标分别为B（0，-b），F（c，0），P（c，

b2

a

），
∵2

OA

=

OF

+

OP

，
∴点A的坐标为(c，

b2

2a

)，
则

OA

=(c，

b2

2a

)，

OB

=(0，-b)，
∵

OA

•

OB

=-

1

4

，∴

b2

2a

 •(-b)=- 

1

4

，即a=2b³．
∵e=

c

a

=

5

2

，∴c=

5

2

a，b=

(  5 2 a)2-a2

=

1

2

a，
∴a=2，b=1，
故双曲线方程为

x2

4

-y2=1．
（2）由题设知直线l的斜率存在，设直线l的方程为y=kx-2，
联立方程组

x2 4 -y2=1 y=kx-2

，得（1-4k²）x²+16kx-20=0，
设M（x₁，y₁），N（x₂，y₂），
由

1-4 k2≠0 △=(16k )2+80(1-4k2)＞0

，解得k2＜

5

4

，且k2≠

1

4

，
∴x1+x2=

16k

4k2-1

，x1x2=

20

4k2-1

，
∴

OM

•

ON

=x1x2+y1y2
=x₁•x₂+（kx₁-2）（kx₂-2）
=（1+k²）x₁x₂-2k（x₁+x₂）+4
=

20(1+k2)

4k2-1

- 

32k2

4k2-1

+4
=

4k2+16

4k2-1

=1+

17

4k2-1

，
∵0≤k2＜

5

4

，且k2≠

1

4

，
∴

17

4k2-1

∈(-∞，-17]∪(

17

4

，+∞)，
∴

OM

•

ON

的范围是(-∞，-16]∪(

21

4

，+∞)．

点评：本题考查直线和双曲线的位置关系的综合运用，考查推理论证能力，考查计算求解能力，考查转化化归思想．解题时要认真审题，仔细解答，注意培养计算能力．