Question

3．若圆${C_1}：{（x-1）^2}+{（y-2）^2}=4$与圆${C_2}：{（x+1）^2}+{y^2}=8$相交于点A，B，则|AB|=$\sqrt{14}$．

Answer 1

分析 求出两圆半径和圆心距，设AM=h，利用勾股定理列方程求出h，从而得出AB．

解答 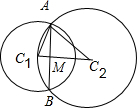解：设AB的中点为M，则AM⊥C₁C₂，
C₁C₂=$\sqrt{（1+1）^{2}+{2}^{2}}$=2$\sqrt{2}$，C₁A=2，C₂A=2$\sqrt{2}$，
设AM=h，则C₁M=$\sqrt{4-{h}^{2}}$，C₂M=$\sqrt{8-{h}^{2}}$，
∴$\sqrt{4-{h}^{2}}$+$\sqrt{8-{h}^{2}}$=2$\sqrt{2}$，解得h=$\frac{\sqrt{14}}{2}$
∴AB=2h=$\sqrt{14}$．
故答案为：$\sqrt{14}$．

点评 本题考查了圆与圆的位置关系，圆的方程，属于中档题．