题目内容
12.证明:函数y=$\sqrt{2x-{x}^{2}}$满足关系式y3y″+1=0.分析 根据导数的运算法则先求导,再求导,代值计算即可.
解答 证明:y=$\sqrt{2x-{x}^{2}}$=(2x-x2)${\;}^{\frac{1}{2}}$,
∴y′=$\frac{1}{2}$(2x-x2)${\;}^{-\frac{1}{2}}$(2x-x2)′=(2x-x2)${\;}^{-\frac{1}{2}}$(1-x),
∴y″=-$\frac{1}{2}$(2x-x2)${\;}^{-\frac{3}{2}}$(2-2x)•(1-x)-(2x-x2)${\;}^{-\frac{1}{2}}$=-(2x-x2)${\;}^{-\frac{3}{2}}$•(1-x)2-(2x-x2)${\;}^{-\frac{1}{2}}$,
∴y3y″+1=[-(2x-x2)${\;}^{-\frac{3}{2}}$•(1-x)2-(2x-x2)${\;}^{-\frac{1}{2}}$]•(2x-x2)${\;}^{\frac{3}{2}}$+1=-(1-x)2-2x+x2+1=-1-x2+2x-2x+x2+1=0
点评 本题考查了导数的运算法则和复合函数的求导法则,以及指数幂的运算性质,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2. 一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:
一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:
①长方形;
②正方形;
③圆.
其中正确的是( )
 一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:
一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;
②正方形;
③圆.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①② |
4.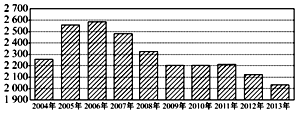 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )| A. | 逐年比较,2005年减少二氧化硫排放量的效果最显著 | |
| B. | 2008年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
1.已知集合A={1,3,$\sqrt{m}$},B={1,m},A∩B={1,m},则m=( )
| A. | 0或$\sqrt{3}$ | B. | 0或3 | C. | 1或3 | D. | 1或3或0 |
2.在等比数列{an}中,若a6=6,a9=9,则a3为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{16}{9}$ | D. | 4 |