题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)y=x-1;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(Ⅰ)当![]() 时,求出切点坐标,然后求出
时,求出切点坐标,然后求出![]() ,从而求出
,从而求出![]() 的值即为切线的斜率,利用点斜式可求出切线方程;
的值即为切线的斜率,利用点斜式可求出切线方程;
(Ⅱ)先求导函数,要使![]() 在定义域(0,+∞)内是增函数,只需
在定义域(0,+∞)内是增函数,只需![]() 在(0,+∞)内恒成立,然后将
在(0,+∞)内恒成立,然后将![]() 分离,利用基本不等式可求出
分离,利用基本不等式可求出![]() 的取值范围;
的取值范围;
(III)根据g(x)在[1,e]上的单调性求出其值域,然后根据(II)可求出![]() 的最大值,要使在[1,e]上至少存在一点x0,使得
的最大值,要使在[1,e]上至少存在一点x0,使得![]() 成立,只需
成立,只需![]() ,x∈[1,e],然后建立不等式,解之即可求出
,x∈[1,e],然后建立不等式,解之即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)当a=1时,函数![]() , ∴f(1)=1-1-ln1=0.
, ∴f(1)=1-1-ln1=0.![]() ,
,
曲线f(x)在点(1,f(1))处的切线的斜率为f'(1)=1+1-1=1.
从而曲线f(x)在点(1,f(1))处的切线方程为y-0=x-1, 即y=x-1.
(2)![]() .
.
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立.
即:ax2-x+a≥0得:![]() 恒成立.
恒成立.
由于![]() , ∴
, ∴![]() , ∴
, ∴![]()
∴f(x)在(0,+∞)内为增函数,实数a的取值范围是![]() .
.
(3)∵![]() 在[1,e]上是减函数
在[1,e]上是减函数
∴x=e时,g(x)min=1,x=1时,g(x)max=e,即g(x)∈[1,e]
f'(x)=![]() 令h(x)=ax2-x+a
令h(x)=ax2-x+a
当![]() 时,由(II)知f(x)在[1,e]上是增函数,f(1)=0<1
时,由(II)知f(x)在[1,e]上是增函数,f(1)=0<1
又![]() 在[1,e]上是减函数,故只需f(x)max≥g(x)min,x∈[1,e]
在[1,e]上是减函数,故只需f(x)max≥g(x)min,x∈[1,e]
而f(x)max=f(e)=![]() ,g(x)min=1,即
,g(x)min=1,即![]() ≥1
≥1
解得a≥![]() ∴实数a的取值范围是[
∴实数a的取值范围是[![]() ,+∞)
,+∞)

【题目】某高中为了解高中学生的性别和喜爱打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜爱打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附: 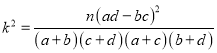
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |