题目内容
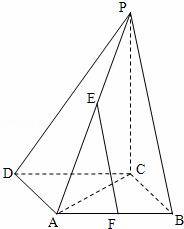
如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，E，F是PA和AB的中点．
（1）求证：EF∥平面PBC；
（2）求E到平面PBC的距离．
（1）证明：∵AE=PE，AF=BF，
∴EF∥PB
又EF⊄平面PBC，PB⊂平面PBC，
故EF∥平面PBC；
（2）解：在面ABCD内作过F作FH⊥BC于H
∵PC⊥面ABCD，PC⊂面PBC
∴面PBC⊥面ABCD
又面PBC∩面ABCD=BC，FH⊥BC，FH⊂面ABCD∴FH⊥面PBC
又EF||平面PBC，故点E到平面PBC的距离等于点F到平面PBC的距离FH．
在直角三角形FBH中，∠FBC=60°，FB=
，FH=FBsin∠FBC=
a，
故点E到平面PBC的距离等于点F到平面PBC的距离，
等于
a．
练习册系列答案
相关题目
中国式过马路，是网友对部分中国人集体闯红灯现象的一种调侃，即“凑够一撮人就可以走了，和红绿灯无关”．某校对全校学生过马路方式进行调查，在所有参与调查的人中，“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示：
|
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 |
| 男生 | 800 | 440 | 200 |
| 女生 | 200 | 160 | 200 |
(1)在所有参与调查的人中，用分层抽样的方法抽取n个人，已知“跟从别人闯红灯”的人中抽取50人，求n的值．
(2)在“带头闯红灯”的人中，将男生的200人编号为001,002，…，200；将女生的200人编号为201,202，…，400，用系统抽样的方法抽取5人参加“文明交通”宣传活动，若抽取的第一个人的编号为30，把抽取的5人看成一个总体，从这5人中任选取2人，求至少有一名女生的概率．
，则m的值是（ ）
，1) C．[0,1] D．[－1，0]