题目内容
10.已知△ABC的外接圆半径为1,圆心为O,且满足$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,则$\overrightarrow{AB}$•$\overrightarrow{OC}$=( )| A. | -$\frac{15}{16}$ | B. | -$\frac{7}{16}$ | C. | $\frac{7}{16}$ | D. | $\frac{15}{16}$ |
分析 先将一个向量用其余两个向量表示出来,然后借助于平方使其出现向量模的平方,则才好用上外接圆半径,然后进一步分析结论,容易化简出要求的结果.
解答 解:由$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,得2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$-\overrightarrow{OA}$,
两边平方得$(2\overrightarrow{OB}+4\overrightarrow{OC})^{2}={\overrightarrow{OA}}^{2}$,即$4{\overrightarrow{OB}}^{2}+16\overrightarrow{OB}•\overrightarrow{OC}+16{\overrightarrow{OC}}^{2}={\overrightarrow{OA}}^{2}$,
得$4+16+16\overrightarrow{OB}•\overrightarrow{OC}=1$,∴$\overrightarrow{OB}•\overrightarrow{OC}=-\frac{19}{16}$;
由$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,得$\overrightarrow{OA}$+4$\overrightarrow{OC}$=-2$\overrightarrow{OB}$,
两边平方得$(\overrightarrow{OA}+4\overrightarrow{OC})^{2}=4{\overrightarrow{OB}}^{2}$,即${\overrightarrow{OA}}^{2}+8\overrightarrow{OA}•\overrightarrow{OC}+16{\overrightarrow{OC}}^{2}=4{\overrightarrow{OB}}^{2}$,
得$1+8\overrightarrow{OA}•\overrightarrow{OC}+16=4$,∴$\overrightarrow{OA}•\overrightarrow{OC}=-\frac{13}{8}$.
∴$\overrightarrow{AB}$•$\overrightarrow{OC}$=$(\overrightarrow{OB}-\overrightarrow{OA})•\overrightarrow{OC}=\overrightarrow{OB}•\overrightarrow{OC}-\overrightarrow{OA}•\overrightarrow{OC}$=$-\frac{19}{16}+\frac{13}{8}=\frac{7}{16}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,是中档题.

| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | c>a>b | B. | b<c<a | C. | a<b<c | D. | a<c<b |
| A. | 19 | B. | 14 | C. | -18 | D. | -19 |
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
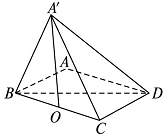 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.