题目内容
解不等式：a2x2+b2（1-x）≥（ax+b（1-x））2．
考点：一元二次不等式的解法,其他不等式的解法
专题：不等式的解法及应用
分析：a2x2+b2（1-x）≥（ax+b（1-x））2．展开化为b（2a-b）x（x-1）≥0．对b（2a-b）分类讨论即可得出．
解答：
解：a2x2+b2（1-x）≥（ax+b（1-x））2．
化为a2x2+b2（1-x）≥a2x2+2abx（1-x）+b2（1-x）2，
化为b（2a-b）x（x-1）≥0．
当b（2a-b）=0时，不等式的解集为R．
当b（2a-b）＞0时，不等式的解集为{x|x≥1或x≤0}．
当b（2a-b）＜0时，不等式的解集为{x|0≤x≤1}．
化为a2x2+b2（1-x）≥a2x2+2abx（1-x）+b2（1-x）2，
化为b（2a-b）x（x-1）≥0．
当b（2a-b）=0时，不等式的解集为R．
当b（2a-b）＞0时，不等式的解集为{x|x≥1或x≤0}．
当b（2a-b）＜0时，不等式的解集为{x|0≤x≤1}．
点评：本题考查了一元二次不等式的解法、分类讨论的思想方法，属于基础题．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
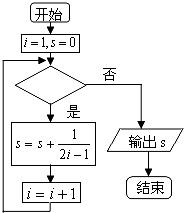如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |
| A、i≤1006 |
| B、i＞1006 |
| C、i≤1007 |
| D、i＞1007 |
复数z满足
=1（i为虚数单位），则复数z为（ ）
| 1-zi |
| i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |