题目内容
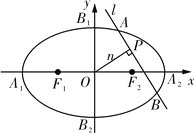
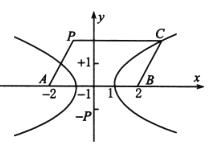
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,(
,( ![]() 为原点)
为原点)
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() :
: ![]() 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) 双曲线![]() 的方程为
的方程为![]() ;(2)
;(2) ![]() 的取值范围为
的取值范围为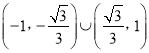 .
.
【解析】试题分析:(1)由题意设出双曲线的方程,再由已知a和c的值求出b2的值,则双曲线C的方程可求;
(2)直接联立直线方程和双曲线方程,化为关于![]() 的方程后由二次项系数不等于0且判别式大于0求解
的方程后由二次项系数不等于0且判别式大于0求解![]() 的取值范围,然后结合
的取值范围,然后结合![]() 得答案.
得答案.
试题解析:(1)设双曲线方程为![]() (
(![]() ,
, ![]() )
)
由已知得![]() ,
, ![]() ,再由
,再由![]() ,得
,得![]() ,所以双曲线
,所以双曲线![]() 的方程为
的方程为![]() .
.
(2)将![]() 代入
代入![]() 得
得
![]() .由直线
.由直线![]() 与双曲线交于不同的两点得
与双曲线交于不同的两点得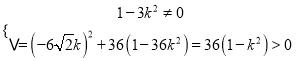 即
即![]() 且
且![]() .①
.①
设![]() 、
、![]() ,则
,则![]() ,
, ![]() ,
,
由![]() 得
得![]() ,而
,而
![]()
![]()
![]()
![]()
于是![]() ,即
,即![]() .解此不等式得
.解此不等式得![]() ,②由①②得
,②由①②得![]()
故![]() 的取值范围为
的取值范围为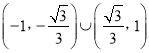 .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目