题目内容
方程ax2+ay2-4(a-1)x+4y=0表示圆,求实数a的取值范围,并求出其中半径最小的圆的方程.
a=2时,圆的半径最小,它的方程为(x-1)2+(y+1)2=2.
原方程化为
.
∵a2-2a+2＞0,
∴当a≠0且a∈R时,原方程表示圆.
∵
,
∴当
,即a=2时,圆的半径最小,它的方程为(x-1)2+(y+1)2="2."
.∵a2-2a+2＞0,
∴当a≠0且a∈R时,原方程表示圆.
∵
,∴当
,即a=2时,圆的半径最小,它的方程为(x-1)2+(y+1)2="2." 
练习册系列答案
阅读快车系列答案
相关题目
=
.
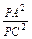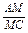，求这个圆的方程
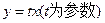则圆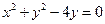
的参数方程为____________________。