题目内容
等差数列{an}中,前m(m为奇数)项的和为99,其中偶数项之和为44,且a1-am=16,则通项公式an= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知得
=11,a1=19,am=3,由此能求出通项公式an.
| a1+am |
| 2 |
解答:
解:偶数项的和44,奇数项的和为=99-44=55
设公差为d
∵奇数项的和-偶数项的和=
=55-44=11,
又am=a1+d(m-1)
∴
=11,
∵a1-am=16,
∴a1=19,am=3,
∵
=99,
∴m=9,
∴d=-
=-2,
∴an=a1+d(n-1)=19-2(n-1)=21-2n.
故答案为:21-2n.
设公差为d
∵奇数项的和-偶数项的和=
| 2a1+(m-1)d |
| 2 |
又am=a1+d(m-1)
∴
| a1+am |
| 2 |
∵a1-am=16,
∴a1=19,am=3,
∵
| m(a1+am) |
| 2 |
∴m=9,
∴d=-
| 16 |
| m-1 |
∴an=a1+d(n-1)=19-2(n-1)=21-2n.
故答案为:21-2n.
点评:本题考查等差数列的通项公式的求法,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
数列
,
,
,
,
,
,…,
,
,…,
,…的前40项的和是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 1 |
| m+1 |
| 2 |
| m+1 |
| m |
| m+1 |
A、23
| ||
B、19
| ||
| C、19 | ||
| D、18 |
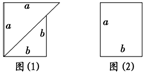 如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为
如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为