题目内容
已知动点P到定点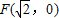 的距离与点P到定直线l:
的距离与点P到定直线l: 的距离之比为
的距离之比为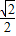 .
.(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E与点F关于原点O对称,若
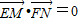 ,求|MN|的最小值.
,求|MN|的最小值.
【答案】分析:(1)先设点P坐标,再根据定点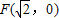 的距离与点P到定直线l:
的距离与点P到定直线l: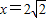 的距离之比为
的距离之比为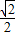 求得方程.
求得方程.
(2))先由点E与点F关于原点O对称,求得E的坐标,再根据直线l的方程设M、N坐标,然后由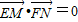 ,即6+y1y2=0.构建
,即6+y1y2=0.构建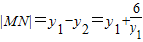 ,再利用基本不等式求得最小值.
,再利用基本不等式求得最小值.
解答:解:(1)设点P(x,y),
依题意,有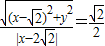 .
.
整理,得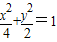 .
.
所以动点P的轨迹C的方程为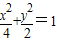 .
.
(2)∵点E与点F关于原点O对称,
∴点E的坐标为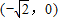 .
.
∵M、N是直线l上的两个点,
∴可设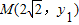 ,
,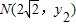 (不妨设y1>y2).
(不妨设y1>y2).
∵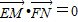 ,
,
∴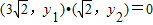 .
.
即6+y1y2=0.即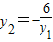 .
.
由于y1>y2,则y1>0,y2<0.
∴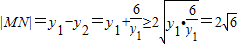 .
.
当且仅当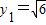 ,
, 时,等号成立.
时,等号成立.
故|MN|的最小值为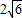 .
.
点评:本小题主要考查椭圆、基本不等式等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力
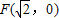 的距离与点P到定直线l:
的距离与点P到定直线l: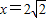 的距离之比为
的距离之比为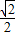 求得方程.
求得方程.(2))先由点E与点F关于原点O对称,求得E的坐标,再根据直线l的方程设M、N坐标,然后由
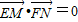 ,即6+y1y2=0.构建
,即6+y1y2=0.构建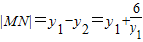 ,再利用基本不等式求得最小值.
,再利用基本不等式求得最小值.解答:解:(1)设点P(x,y),
依题意,有
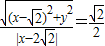 .
.整理,得
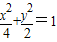 .
.所以动点P的轨迹C的方程为
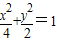 .
.(2)∵点E与点F关于原点O对称,
∴点E的坐标为
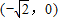 .
.∵M、N是直线l上的两个点,
∴可设
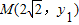 ,
,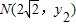 (不妨设y1>y2).
(不妨设y1>y2).∵
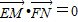 ,
,∴
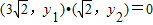 .
.即6+y1y2=0.即
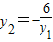 .
.由于y1>y2,则y1>0,y2<0.
∴
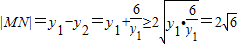 .
.当且仅当
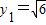 ,
, 时,等号成立.
时,等号成立.故|MN|的最小值为
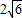 .
.点评:本小题主要考查椭圆、基本不等式等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 的距离d1,是到定点F(-
的距离d1,是到定点F(- )的距离d2的
)的距离d2的 倍.
倍.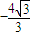 的距离d1,是到定点F(-
的距离d1,是到定点F(-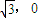 )的距离d2的
)的距离d2的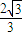 倍.
倍.