题目内容
已知动点P到直线l:x=- 的距离d1,是到定点F(-
的距离d1,是到定点F(- )的距离d2的
)的距离d2的 倍.
倍.(1) 求动点P的轨迹方程;
(2) 若直线m:y=k(x+1)(k≠o)与点P的轨迹有两个交点A、B,求弦AB的中垂线n在y轴上的截距y的取值范围.
【答案】分析:(1)设P(x,y),则 ,由题设知
,由题设知 ,由此能求出动点P的轨迹方程.
,由此能求出动点P的轨迹方程.
(2)将y=k(x+1)(k≠0)代入 ,消去y,得(1+4k2)x2+8k2x+4k2-4=0,设A(x1,y1),B(x2,y2),则
,消去y,得(1+4k2)x2+8k2x+4k2-4=0,设A(x1,y1),B(x2,y2),则 ,
, ,弦AB的中点为
,弦AB的中点为 ,中垂线n的方程为
,中垂线n的方程为 ,由此能求出y的取值范围.
,由此能求出y的取值范围.
解答:解:(1)设P(x,y),则 ,
,
由题设知 ,
,
平方整理可得 .
.
(2)将y=k(x+1)(k≠0)代入 ,
,
消去y,得(1+4k2)x2+8k2x+4k2-4=0,
设A(x1,y1),B(x2,y2),则 ,
,
 ,
,
弦AB的中点为 ,中垂线n的方程为
,中垂线n的方程为 ,
,
令x=0,可得 ,
,
∵ ,
, 或
或 ,
,
∴ ,且
,且 ,
,
即y的取值范围是 .
.
点评:本题考查直线 和椭圆的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件.
 ,由题设知
,由题设知 ,由此能求出动点P的轨迹方程.
,由此能求出动点P的轨迹方程.(2)将y=k(x+1)(k≠0)代入
 ,消去y,得(1+4k2)x2+8k2x+4k2-4=0,设A(x1,y1),B(x2,y2),则
,消去y,得(1+4k2)x2+8k2x+4k2-4=0,设A(x1,y1),B(x2,y2),则 ,
, ,弦AB的中点为
,弦AB的中点为 ,中垂线n的方程为
,中垂线n的方程为 ,由此能求出y的取值范围.
,由此能求出y的取值范围.解答:解:(1)设P(x,y),则
 ,
,由题设知
 ,
,平方整理可得
 .
.(2)将y=k(x+1)(k≠0)代入
 ,
,消去y,得(1+4k2)x2+8k2x+4k2-4=0,
设A(x1,y1),B(x2,y2),则
 ,
, ,
,弦AB的中点为
 ,中垂线n的方程为
,中垂线n的方程为 ,
,令x=0,可得
 ,
,∵
 ,
, 或
或 ,
,∴
 ,且
,且 ,
,即y的取值范围是
 .
.点评:本题考查直线 和椭圆的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
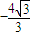 的距离d1,是到定点F(-
的距离d1,是到定点F(-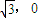 )的距离d2的
)的距离d2的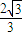 倍.
倍.