题目内容
已知动点P到直线![]() 的距离是到定点(
的距离是到定点(![]() )的距离的
)的距离的![]() 倍.
倍.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)如果直线l∶y=k(x+1)(k≠0)与P点的轨迹有两个交点A、B,求弦AB的垂直平分线在y轴上的截距y0的取值范围.
答案:
解析:
解析:
解:(Ⅰ)设动点P(x,y),由题意知![]() .
.
∴![]() .
.
即动点P的轨迹方程是![]() .
.
(Ⅱ)联立方程组
得:![]() .
.
从而
弦AB的中点坐标为:![]()
弦AB的线段垂直平分线方程为![]() .
.
所以垂直平分线在y轴上的截距为:![]() ,(k≠0).
,(k≠0).
故弦AB的线段垂直平分线在y轴上的截距的取值范围为![]() .
.
命题意图:对解析几何两大基本问题:①求轨迹;②通过方程研究曲线性质进行再梳理.轨迹方程的求法一般分为直接法和间接法.直接法的步骤:建系设点,找等量关系,列方程,化简,检验;间接法的关键是找参数.如果明确说直线与圆锥曲线有两个不同的交点,一般是考查判别式与根系关系的应用.取值范围一般是函数的值域或不等式(组)的解集.

练习册系列答案
相关题目
 的距离d1,是到定点F(-
的距离d1,是到定点F(- )的距离d2的
)的距离d2的 倍.
倍.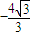 的距离d1,是到定点F(-
的距离d1,是到定点F(-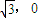 )的距离d2的
)的距离d2的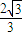 倍.
倍.