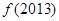题目内容
已知函数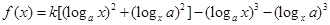 ,
, ,(其中
,(其中 ),设
),设 .
.
(Ⅰ)当 时,试将
时,试将 表示成
表示成 的函数
的函数 ,并探究函数
,并探究函数 是否有极值;
是否有极值;
(Ⅱ)当 时,若存在
时,若存在 ,使
,使 成立,试求
成立,试求 的范围.
的范围.
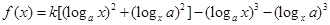 ,
, ,(其中
,(其中 ),设
),设 .
.(Ⅰ)当
 时,试将
时,试将 表示成
表示成 的函数
的函数 ,并探究函数
,并探究函数 是否有极值;
是否有极值;(Ⅱ)当
 时,若存在
时,若存在 ,使
,使 成立,试求
成立,试求 的范围.
的范围.(Ⅰ)当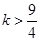 时
时 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当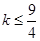 时
时 在定义域内无极值;
在定义域内无极值;
(Ⅱ)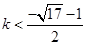 或
或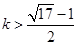
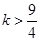 时
时 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当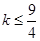 时
时 在定义域内无极值;
在定义域内无极值;(Ⅱ)
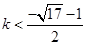 或
或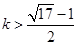
试题分析:(Ⅰ)观察
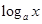 与
与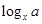 的特点
的特点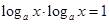 ,可得
,可得 ,
,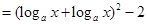 ,
,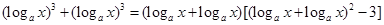 ,即可得到函数
,即可得到函数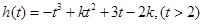 ,观察此函数特征可想到对其求导得
,观察此函数特征可想到对其求导得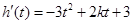 ,由二次函数的图象不难得出
,由二次函数的图象不难得出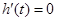 在
在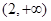 上有解的条件
上有解的条件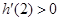 ,进而求出
,进而求出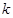 的范围; (Ⅱ)由
的范围; (Ⅱ)由 可得
可得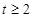 ,又由
,又由 可得
可得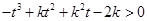 ,故可令函数
,故可令函数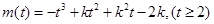 的最大值为正,对函数求导令其为0得
的最大值为正,对函数求导令其为0得 求出
求出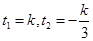 ,由
,由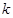 与
与 ,和
,和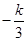 与
与 的大小关系对
的大小关系对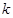 进行分类讨论,并求出各自情况的最大值,由最大值大于零即可求出
进行分类讨论,并求出各自情况的最大值,由最大值大于零即可求出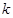 的范围.
的范围.试题解析:(Ⅰ)∵
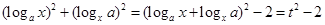 ,
,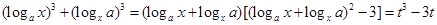 ,
,∴
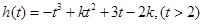 ∴
∴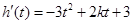 (3分)
(3分)设
 是
是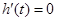 的两根,则
的两根,则 ,∴
,∴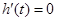 在定义域内至多有一解,
在定义域内至多有一解,欲使
 在定义域内有极值,只需
在定义域内有极值,只需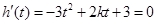 在
在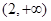 内有解,且
内有解,且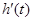 的值在根的左右两侧异号,∴
的值在根的左右两侧异号,∴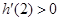 得
得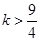 (6分)
(6分)综上:当
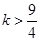 时
时 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当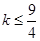 时
时 在定义域内无极值.
在定义域内无极值.(Ⅱ)∵存在
 ,使
,使 成立等价于
成立等价于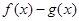 的最大值大于0,
的最大值大于0,∵
 ,∴
,∴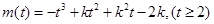 ,
,∴
 得
得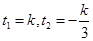 .
.当
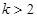 时,
时,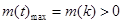 得
得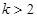 ;
;当
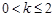 时,
时,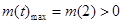 得
得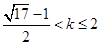 (12分)
(12分)当
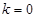 时,
时,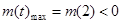 不成立 (13分)
不成立 (13分)当
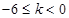 时,
时,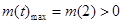 得
得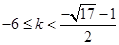 ;
;当
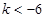 时,
时, 得
得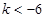 ;
;综上得:
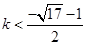 或
或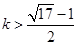 (16分)
(16分)
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 .
. ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数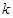 的取值范围;
的取值范围; ,
,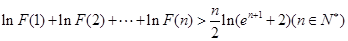
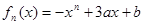 (
(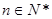 ,
,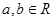 )。
)。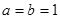 ,求
,求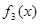 在
在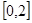 上的最大值和最小值;
上的最大值和最小值;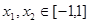 ,都有
,都有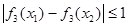 ,求
,求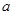 的取值范围;
的取值范围;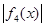 在
在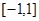 上的最大值为
上的最大值为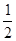 ,求
,求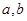 的值。
的值。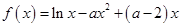 .
.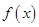 在
在 处取得极值,求实数
处取得极值,求实数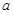 的值;
的值;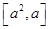 上的最大值.
上的最大值. 在
在 上是增函数,
上是增函数, 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.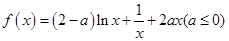 .
.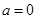 时,求
时,求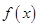 的极值;(2)当
的极值;(2)当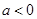 时,讨论
时,讨论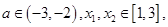 恒有
恒有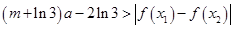 成立,求实数
成立,求实数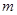 的取值范围.
的取值范围. 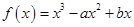 的图象与直线
的图象与直线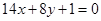 相切于点
相切于点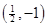 .
.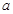 和
和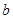 的值; (2)求
的值; (2)求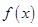 的极值.
的极值. ,
, (
( ,
, 为自然对数的底数).
为自然对数的底数). 时,求
时,求 的单调区间;
的单调区间; ,
, 恒成立,求
恒成立,求 的最小值;
的最小值; ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求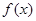 为R上的可导函数,且
为R上的可导函数,且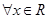 ,均有
,均有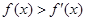 ,则有 ( )
,则有 ( )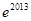
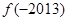
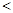
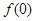 ,
,