题目内容
用0.618法选取试点的过程中．如果实验区间为[1000，2000]，前三个试点依次为x1，x2，x3（x2＜x1）；且x2比x1处的试验结果好，则x3= ．
考点：优选法的概念
专题：选作题,函数的性质及应用
分析：确定区间长度，利用0.618法选取试点，即可求得结论．
解答：
解：由已知试验范围为[1000，2000]，可得区间长度为1000，
利用0.618法选取试点：x1=1000+0.618×（2000-1000）=1618，x2=1000+2000-1618=1382，
∵x2处的结果比x1处好，
∴x3=1618+1000-1382=1236．
故答案为：1236．
利用0.618法选取试点：x1=1000+0.618×（2000-1000）=1618，x2=1000+2000-1618=1382，
∵x2处的结果比x1处好，
∴x3=1618+1000-1382=1236．
故答案为：1236．
点评：本题考查的是黄金分割法-0.618法的简单应用．解答的关键是要了解黄金分割法-0.618法．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
某单位安排2013年春节期间7天假期的值班情况，7个员工每人各值一天．已知某员工甲必须排在前两天，员工乙不能排在第一天，员工丙必须排在最后一天，则不同的值班顺序有（ ）
| A、120种 | B、216种 |
| C、720种 | D、540种 |
复数z=
的共轭复数的虚部为（ ）
| 4+3i |
| 2-i |
| A、-2 | B、-2i | C、2 | D、2i |
下列对程序框图的描述，正确的是（ ）
| A、只有一个起点，一个终点 |
| B、只有一个起点，一个或多个终点 |
| C、多个起点，一个或多个终点 |
| D、多个起点，只有一个终点 |
已知sinα=-
，且α是第四象限角，则tanα的值为（ ）
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
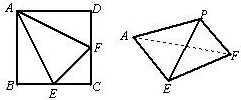正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P，则P到面AEF的距离为