题目内容
7．已知函数f（x）=2017x+log2017（$\sqrt{{x}^{2}+1}$+x）-2017-x，则关于x的不等式f（2x+3）+f（x）＞0的解集是（ ）| A． | （-3，+∞） | B． | （-∞，-3） | C． | （-∞，-1） | D． | （-1，+∞） |
分析 根据题意，对于f（x）=2017x+log2017（$\sqrt{{x}^{2}+1}$+x）-2017-x，分析其奇偶性与单调性，可得f（x）为奇函数且增函数，从而原不等式可以转化为2x+3＞-x，解可得x的取值范围，即可得答案．
解答 解：根据题意，对于f（x）=2017x+log2017（$\sqrt{{x}^{2}+1}$+x）-2017-x，
其定义域为R，关于原点对称，f（-x）=2017-x+log2017（$\sqrt{{x}^{2}+1}$-x）-2017x
=-（2017x+log2017（$\sqrt{{x}^{2}+1}$+x）-2017-x）=-f（x）；
即函数f（x）为奇函数；
对于f（x）=2017x+log2017（$\sqrt{{x}^{2}+1}$+x）-2017-x，分析易得其为增函数；
f（2x+3）+f（x）＞0?f（2x+3）＞-f（x）?f（2x+3）＞f（-x）?2x+3＞-x，
解可得x＞-1；
即不等式f（2x+3）+f（x）＞0的解集是（-1，+∞），
故选：D．
点评 本题考查函数的奇偶性与单调性的综合应用，关键是分析函数f（x）的奇偶性与单调性．
练习册系列答案
相关题目
17．
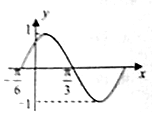函数f（x）=sin（ωx+φ）（x∈R，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，如果x1+x2=$\frac{2π}{3}$，则f（x1）+f（x2）=（ ）
函数f（x）=sin（ωx+φ）（x∈R，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，如果x1+x2=$\frac{2π}{3}$，则f（x1）+f（x2）=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | 0 | D． | -$\frac{1}{2}$ |
18．若将函数y=sin（6x+$\frac{π}{4}$）图象上各点的横坐标伸长到原来的3倍（纵坐标不变），再将所得图象沿x轴向右平移$\frac{π}{8}$个单位长度，则所得图象的一个对称中心是（ ）
| A． | （$\frac{π}{16}$，0） | B． | （$\frac{π}{9}$，0） | C． | （$\frac{π}{4}$，0） | D． | （$\frac{π}{2}$，0） |
2．已知i为虚数单位，若复数z满足i3•z=1+i，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | 2 | D． | $\sqrt{3}$ |
已知一个正△ABC的边长为6cm，点D到△ABC各顶点的距离都是4cm．求：