题目内容
已知椭圆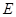 :
: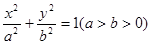 的左焦点
的左焦点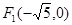 ,若椭圆上存在一点
,若椭圆上存在一点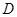 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段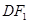 相切于线段
相切于线段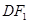 的中点
的中点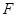 .
.
(Ⅰ)求椭圆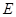 的方程;
的方程;
(Ⅱ)已知两点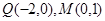 及椭圆
及椭圆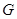 :
: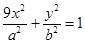 ,过点
,过点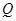 作斜率为
作斜率为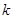 的直线
的直线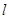 交椭圆
交椭圆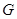 于
于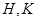 两点,设线段
两点,设线段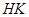 的中点为
的中点为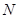 ,连结
,连结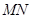 ,试问当
,试问当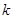 为何值时,直线
为何值时,直线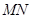 过椭圆
过椭圆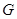 的顶点?
的顶点?
(Ⅲ) 过坐标原点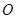 的直线交椭圆
的直线交椭圆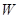 :
: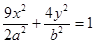 于
于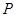 、
、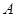 两点,其中
两点,其中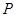 在第一象限,过
在第一象限,过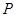 作
作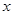 轴的垂线,垂足为
轴的垂线,垂足为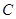 ,连结
,连结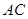 并延长交椭圆
并延长交椭圆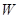 于
于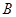 ,求证:
,求证: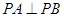
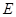 :
: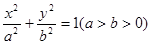 的左焦点
的左焦点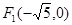 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段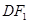 相切于线段
相切于线段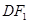 的中点
的中点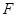 .
.(Ⅰ)求椭圆
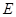 的方程;
的方程;(Ⅱ)已知两点
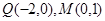 及椭圆
及椭圆 :
: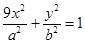 ,过点
,过点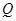 作斜率为
作斜率为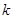 的直线
的直线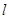 交椭圆
交椭圆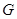 于
于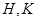 两点,设线段
两点,设线段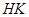 的中点为
的中点为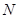 ,连结
,连结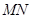 ,试问当
,试问当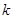 为何值时,直线
为何值时,直线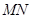 过椭圆
过椭圆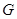 的顶点?
的顶点?(Ⅲ) 过坐标原点
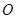 的直线交椭圆
的直线交椭圆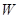 :
: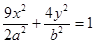 于
于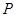 、
、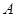 两点,其中
两点,其中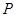 在第一象限,过
在第一象限,过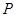 作
作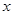 轴的垂线,垂足为
轴的垂线,垂足为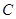 ,连结
,连结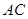 并延长交椭圆
并延长交椭圆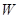 于
于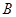 ,求证:
,求证: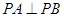
(Ⅰ)连接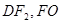
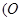 为坐标原点,
为坐标原点,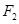 为右焦点),由题意知:椭圆的右焦点为
为右焦点),由题意知:椭圆的右焦点为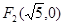 因为
因为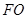 是
是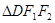 的中位线,且
的中位线,且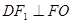 ,所以
,所以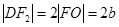
所以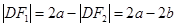 ,故
,故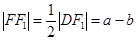 …………2分
…………2分
在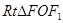 中,
中,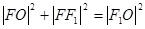
即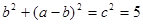 ,又
,又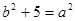 ,解得
,解得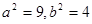
所求椭圆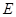 的方程为
的方程为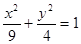 .………………………4分
.………………………4分
(Ⅱ) 由(Ⅰ)得椭圆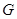 :
: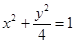
设直线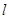 的方程为
的方程为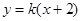 并代入
并代入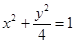
整理得: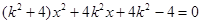
由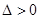 得:
得: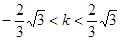 ……………………5分
……………………5分
设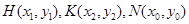
则由中点坐标公式得: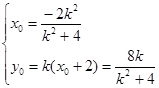 …………………6分
…………………6分
①当 时,有
时,有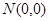 ,直线
,直线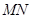 显然过椭圆
显然过椭圆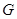 的两个顶点
的两个顶点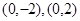 ;………7分
;………7分
②当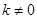 时,则
时,则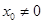 ,直线
,直线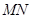 的方程为
的方程为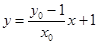
此时直线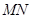 显然不能过椭圆
显然不能过椭圆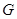 的两个顶点
的两个顶点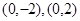 ;
;
若直线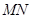 过椭圆
过椭圆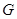 的顶点
的顶点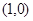 ,则
,则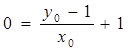 即
即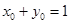
所以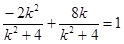 ,解得:
,解得: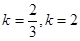 (舍去)………………………8分
(舍去)………………………8分
若直线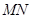 过椭圆
过椭圆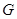 的顶点
的顶点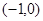 ,则
,则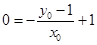 即
即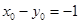
所以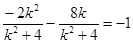 ,解得:
,解得: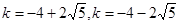 (舍去) ……………9分
(舍去) ……………9分
综上,当 或
或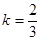 或
或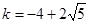 时, 直线
时, 直线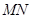 过椭圆
过椭圆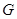 的顶点…………10分
的顶点…………10分
(Ⅲ)法一:由(Ⅰ)得椭圆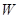 的方程为
的方程为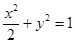 ……………………………11分
……………………………11分
根据题意可设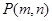 ,则
,则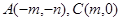
则直线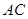 的方程为
的方程为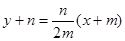 …①
…①
过点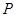 且与
且与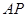 垂直的直线方程为
垂直的直线方程为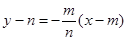 …②
…②
①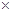 ②并整理得:
②并整理得: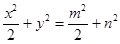
又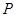 在椭圆
在椭圆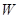 上,所以
上,所以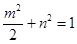 所以
所以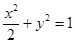
即①、②两直线的交点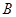 在椭圆
在椭圆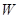 上,所以
上,所以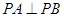 .…………14分
.…………14分
法二:由(Ⅰ)得椭圆 的方程为
的方程为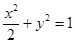
根据题意可设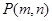 ,则
,则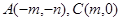 ,
,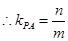 ,
,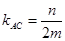
所以直线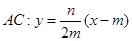
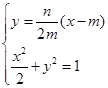 ,化简得
,化简得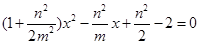
所以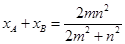
因为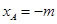 ,所以
,所以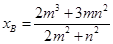 ,则
,则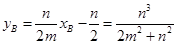 ……………12分
……………12分
所以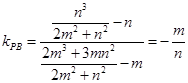 ,则
,则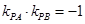 ,即
,即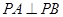
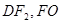
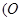 为坐标原点,
为坐标原点,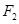 为右焦点),由题意知:椭圆的右焦点为
为右焦点),由题意知:椭圆的右焦点为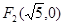 因为
因为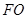 是
是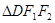 的中位线,且
的中位线,且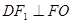 ,所以
,所以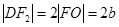
所以
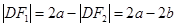 ,故
,故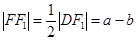 …………2分
…………2分在
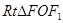 中,
中,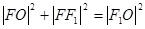
即
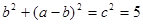 ,又
,又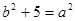 ,解得
,解得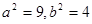
所求椭圆
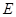 的方程为
的方程为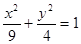 .………………………4分
.………………………4分(Ⅱ) 由(Ⅰ)得椭圆
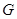 :
: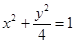
设直线
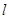 的方程为
的方程为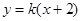 并代入
并代入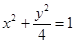
整理得:
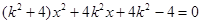
由
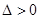 得:
得: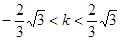 ……………………5分
……………………5分设
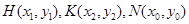
则由中点坐标公式得:
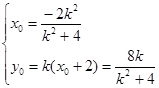 …………………6分
…………………6分①当
 时,有
时,有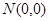 ,直线
,直线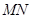 显然过椭圆
显然过椭圆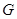 的两个顶点
的两个顶点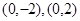 ;………7分
;………7分②当
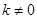 时,则
时,则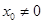 ,直线
,直线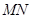 的方程为
的方程为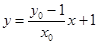
此时直线
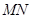 显然不能过椭圆
显然不能过椭圆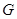 的两个顶点
的两个顶点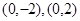 ;
;若直线
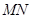 过椭圆
过椭圆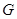 的顶点
的顶点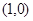 ,则
,则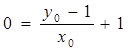 即
即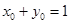
所以
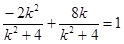 ,解得:
,解得: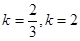 (舍去)………………………8分
(舍去)………………………8分若直线
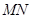 过椭圆
过椭圆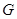 的顶点
的顶点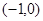 ,则
,则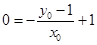 即
即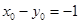
所以
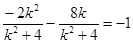 ,解得:
,解得: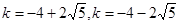 (舍去) ……………9分
(舍去) ……………9分综上,当
 或
或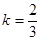 或
或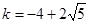 时, 直线
时, 直线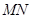 过椭圆
过椭圆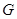 的顶点…………10分
的顶点…………10分(Ⅲ)法一:由(Ⅰ)得椭圆
 的方程为
的方程为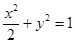 ……………………………11分
……………………………11分根据题意可设
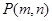 ,则
,则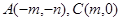
则直线
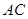 的方程为
的方程为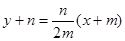 …①
…①过点
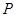 且与
且与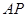 垂直的直线方程为
垂直的直线方程为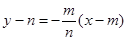 …②
…②①
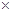 ②并整理得:
②并整理得: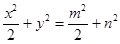
又
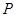 在椭圆
在椭圆 上,所以
上,所以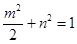 所以
所以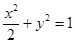
即①、②两直线的交点
 在椭圆
在椭圆 上,所以
上,所以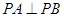 .…………14分
.…………14分法二:由(Ⅰ)得椭圆
 的方程为
的方程为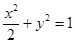
根据题意可设
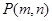 ,则
,则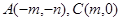 ,
,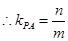 ,
,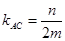
所以直线
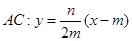
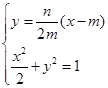 ,化简得
,化简得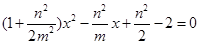
所以
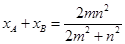
因为
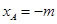 ,所以
,所以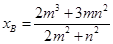 ,则
,则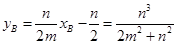 ……………12分
……………12分所以
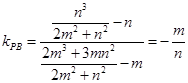 ,则
,则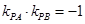 ,即
,即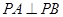
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
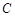 上动点
上动点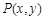 到定点
到定点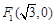 与定直线
与定直线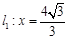 的距离之比为常数
的距离之比为常数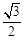 .
.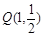 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点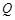 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;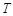 为圆心作圆
为圆心作圆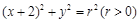 ,设圆
,设圆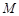 与点
与点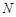 ,求
,求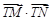 的最小值,并求此时圆
的最小值,并求此时圆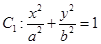 (a>b>0)与双曲线
(a>b>0)与双曲线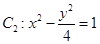 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于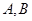 两点.若C1恰好将线段
两点.若C1恰好将线段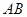 三等分,则
三等分,则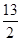
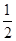
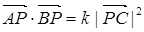 .
.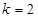 时,求
时,求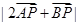 的最大、最小值.
的最大、最小值.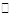 O方程为
O方程为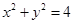 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上,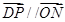 .且
.且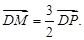
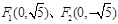 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求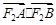 的取值范围.
的取值范围.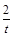 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.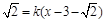 的距离为
的距离为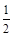 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.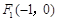 、
、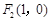 两点的距离之和等于2,则动点M的轨迹是椭圆;②在平面内,给出点
两点的距离之和等于2,则动点M的轨迹是椭圆;②在平面内,给出点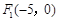 、
、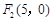 ,若动点P满足
,若动点P满足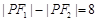 ,则动点P的轨迹是双曲线;③在平面内,若动点Q到点
,则动点P的轨迹是双曲线;③在平面内,若动点Q到点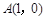 和到直线
和到直线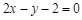 的距离相等,则动点Q的轨迹是抛物线。其中正确的命题有( )
的距离相等,则动点Q的轨迹是抛物线。其中正确的命题有( )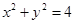 上各点的纵坐标缩短到原来的
上各点的纵坐标缩短到原来的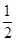 (横坐标不变),所得曲线的方程是( )
(横坐标不变),所得曲线的方程是( )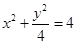
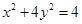
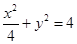
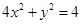
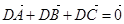 ;②|
;②|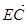 |=
|=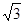 |
|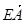 |=
|=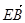 |③
|③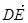 与
与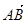 共线.
共线.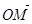 ·
·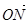 =0,求直线l的方程.
=0,求直线l的方程.