题目内容
已知动圆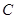 过定点(1,0),且与直线
过定点(1,0),且与直线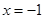 相切.
相切.
(1)求动圆圆心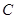 的轨迹方程;
的轨迹方程;
(2)设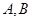 是轨迹
是轨迹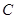 上异于原点
上异于原点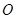 的两个不同点,直线
的两个不同点,直线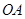 和
和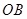 的倾斜角分别为
的倾斜角分别为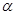 和
和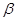 ,①当
,①当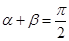 时,求证直线
时,求证直线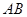 恒过一定点
恒过一定点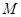 ;
;
②若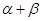 为定值
为定值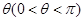 ,直线
,直线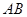 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
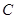 过定点(1,0),且与直线
过定点(1,0),且与直线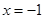 相切.
相切.(1)求动圆圆心
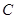 的轨迹方程;
的轨迹方程;(2)设
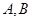 是轨迹
是轨迹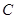 上异于原点
上异于原点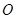 的两个不同点,直线
的两个不同点,直线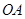 和
和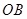 的倾斜角分别为
的倾斜角分别为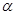 和
和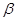 ,①当
,①当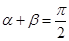 时,求证直线
时,求证直线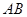 恒过一定点
恒过一定点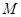 ;
;②若
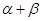 为定值
为定值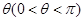 ,直线
,直线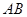 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.(1)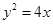 ;(2)①参考解析,②
;(2)①参考解析,②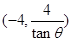
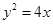 ;(2)①参考解析,②
;(2)①参考解析,②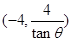
试题分析:(1)根据题意可假设抛物线方程为
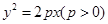 ,由抛物线的定义可求得
,由抛物线的定义可求得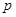 的值,从而可求得抛物线的方程.
的值,从而可求得抛物线的方程.(2)根据题意假设直线AB的方程,联立抛物线的方程,消去y得到一个关于x的一元二次方程,由韦达定理得到A,B两点坐标的等式.①由直线的垂直可得到A,B坐标的一个等式,从而可化简直线AB的方程即可得到结论.②当
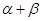 为一个一般的定值时,需要分类讨论,解决问题的方法类似于①小题,同样是通过A,B的斜率关系得到一个等式,从而得到结论.
为一个一般的定值时,需要分类讨论,解决问题的方法类似于①小题,同样是通过A,B的斜率关系得到一个等式,从而得到结论.试题解析:(1)设动圆圆心M(x,y),
依题意点M的轨迹是以(1,0)为焦点,直线x=-1为准线的抛物线其方程为
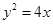 .
.(2)设A(x1,y1),B(x2,y2).由题意得x1≠x2(否则
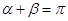 )且x1x2≠0,则
)且x1x2≠0,则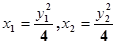
所以直线AB的斜率存在,设直线AB的方程为y=kx+b,
则将y=kx+b与y2=4x联立消去x,得ky2-4y+4b=0
由韦达定理得
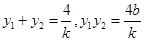 -------※
-------※①当
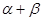 =
=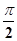 时,
时,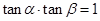 所以
所以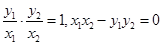 ,所以y1y2=16,又由※知:y1y2=
,所以y1y2=16,又由※知:y1y2=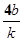 所以b=4k;因此直线AB的方程可表示为y=kx+4k,所以直线AB恒过定点(-4,0).
所以b=4k;因此直线AB的方程可表示为y=kx+4k,所以直线AB恒过定点(-4,0).②当
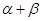 为定值
为定值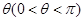 时.若
时.若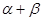 =
=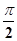 ,由①知,
,由①知,直线AB恒过定点M(-4,0)当
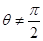 时,由
时,由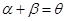 ,得
,得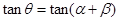 =
=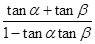 =
=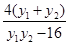
将※式代入上式整理化简可得:
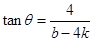 ,所以
,所以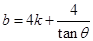 ,此时,直线AB的方程可表示为y=kx+
,此时,直线AB的方程可表示为y=kx+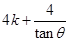 ,所以直线AB恒过定点
,所以直线AB恒过定点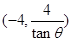 所以当
所以当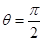 时,直线AB恒过定点(-4,0).,
时,直线AB恒过定点(-4,0).,当
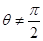 时直线AB恒过定点
时直线AB恒过定点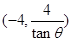

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
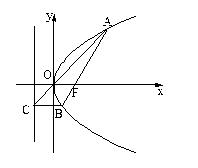
 满足:点P到定点
满足:点P到定点 与到y轴的距离之差为
与到y轴的距离之差为 .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C. 于点D,求证:直线DB平行于x轴.
于点D,求证:直线DB平行于x轴.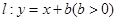 ,抛物线
,抛物线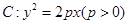 ,已知点
,已知点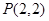 在抛物线
在抛物线 上,且抛物线
上,且抛物线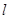 的距离的最小值为
的距离的最小值为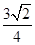 .
.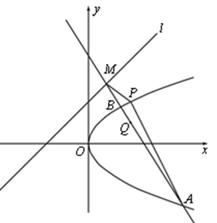
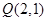 的任一直线(不经过点
的任一直线(不经过点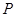 )与抛物线
)与抛物线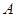 、
、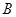 两点,直线
两点,直线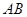 与直线
与直线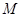 ,记直线
,记直线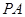 ,
,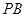 ,
,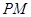 的斜率分别为
的斜率分别为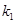 ,
,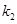 ,
, 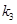 .问:是否存在实数
.问:是否存在实数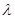 ,使得
,使得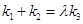 ?若存在,试求出
?若存在,试求出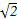
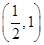
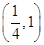
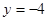 ,则抛物线的标准方程为( )
,则抛物线的标准方程为( )