题目内容
14.已知函数f(x)=2sinωxcosωx+2$\sqrt{3}$sin2ωx-$\sqrt{3}$(ω>0)的最小正周期为π.(1)求函数f(x)的单调增区间;
(2)f(x)的图象是由y=sinx的图象通过怎样平移而得到的;
(3)将函数f(x)的图象向左平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
分析 (1)由三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2ωx-$\frac{π}{3}$),利用周期公式可求ω,
令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2},k∈Z$,即可解得函数f(x)的单调增区间.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(3)由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得g(x)的解析式,再由y=g(x)在[0,b](b>0)上至少含有10个零点,可得方程sin2x=-$\frac{1}{2}$至少有10个解,则b的最小值4×π+$\frac{11π}{12}$,计算可得结果.
解答 解:(1)由题意得f(x)=2sinωxcosωx+2$\sqrt{3}$sin2ωx-$\sqrt{3}$=sin2ωx-$\sqrt{3}$cos2ωx=2sin(2ωx-$\frac{π}{3}$),
由最小正周期为π,得ω=1,
所以$f(x)=2sin(2x-\frac{π}{3})$,
由$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2},k∈Z$,整理得$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12},k∈Z$,
所以函数f(x)的单调增区间是$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}],k∈Z$.
(2)将y=sinx的图象先向右平移$\frac{π}{3}$个单位,得到$y=sin(x-\frac{π}{3})$的图象,
再把各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变,得$y=sin(2x-\frac{π}{3})$,
最后把各点的纵坐标扩大到原来的2倍,横坐标不变得$f(x)=2sin(2x-\frac{π}{3})$的图象.
(或者将y=sinx的图象各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变,得到y=sin2x的图象,
再把所得的图象先向右平移$\frac{π}{6}$个单位,得到$y=sin(2x-\frac{π}{3})$的图象,
最后把各点的纵坐标扩大到原来的2倍,横坐标不变得$f(x)=2sin(2x-\frac{π}{3})$的图象).
(3)将函数f(x)的图象向左平移$\frac{π}{6}$个单位,再向上平移1个单位,得到y=2sin2x+1的图象,
所以g(x)=2sin2x+1,
令g(x)=0,得$x=kπ+\frac{7π}{12}$或$x=kπ+\frac{11π}{12}(k∈Z)$,
所以在[0,π]上恰好有两个零点,
若y=g(x)在[0,b]上有10个零点,
则b不小于第10个零点的横坐标即可,即b的最小值为4π+$\frac{11π}{12}$=$\frac{59π}{12}$.
点评 本题主要考查了三角函数中的恒等变换应用,复合三角函数的单调性,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的特征,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | (-∞,4] | B. | [4,+∞) | C. | [4,5) | D. | [4,5] |
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
| A. | {-3,-2,-1,0} | B. | {-2,-1,0} | C. | {-3,-2,-1,0,1} | D. | {-2,-1,0,1} |
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
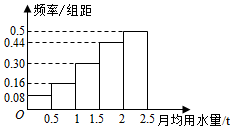 如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨.
如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨.