题目内容
20.已知点M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),若椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,则椭圆C的离心率的取值范围是( )| A. | (0,1) | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$] |
分析 由已知得椭圆C:$\frac{{x}^{2}}{a}$+y2=1与双曲线$\frac{{x}^{2}}{2}-{y}^{2}$=1(x≥$\sqrt{2}$)有交点,由此能求出椭圆C的离心率的取值范围.
解答 解:∵M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,
∴椭圆C:$\frac{{x}^{2}}{a}$+y2=1与双曲线$\frac{{x}^{2}}{2}-{y}^{2}$=1(x≥$\sqrt{2}$)有交点,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\\{\frac{{x}^{2}}{2}-{y}^{2}=1,(x≥\sqrt{2})}\end{array}\right.$,得x2=$\frac{4{a}^{2}}{2+{a}^{2}}$,
∵椭圆C:$\frac{{x}^{2}}{a}$+y2=1与双曲线$\frac{{x}^{2}}{2}-{y}^{2}$=1(x≥$\sqrt{2}$)有交点,
∴x2=$\frac{4{a}^{2}}{2+{a}^{2}}$≥2,解得a$≥\sqrt{2}$,
∵c=$\sqrt{a-1}$,∴$e=\frac{\sqrt{a-1}}{\sqrt{a}}$≥$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
又0<e<1,∴e的取值范围是[$\frac{\sqrt{2}}{2}$,1).
故选:C.
点评 本题考查椭圆离心率的取值范围的求法,是中档题,解题时要认真审题,注意双曲线、椭圆性质的合理运用.

 计算高手系列答案
计算高手系列答案| A. | (-∞,0) | B. | $({-∞,\frac{1}{4}})$ | C. | $({\frac{1}{2},+∞})$ | D. | $({\frac{1}{4},+∞})$ |
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{1}{2}$,1) |
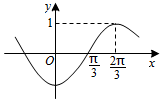
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
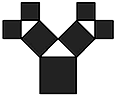 如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.
如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.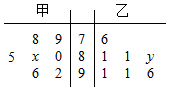 某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )