题目内容
 三角函数式:①
三角函数式:① ,②
,② ,③
,③ ,④
,④ .
.
其中在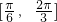 上的图象如图所示的函数是
上的图象如图所示的函数是
- A.③
- B.①②
- C.①②④
- D.①②③④
B
分析:由函数的图象知函数的周期为π,且函数在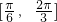 上是增函数,对于③中的函数,当x=
上是增函数,对于③中的函数,当x= 时,y=-3sin
时,y=-3sin ≠-3,对于④中的函数,当x=
≠-3,对于④中的函数,当x= 时,y=-3sin π=0≠-3,故排除③和④.
时,y=-3sin π=0≠-3,故排除③和④.
解答:由函数的图象知函数的周期为π,且函数在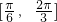 上是增函数.
上是增函数.
由 2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,可得 kπ+
,可得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,故①中的函数在
,k∈z,故①中的函数在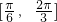 上是增函数.
上是增函数.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得 kπ-
,可得 kπ- ≤x≤kπ-
≤x≤kπ- ,k∈z,故②中的函数在
,k∈z,故②中的函数在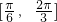 上是增函数.
上是增函数.
综上,①②都满足这两个条件.
对于③中的函数,当x= 时,y=-3sin
时,y=-3sin ≠-3,故此图象不是③中的函数图象,故排除③.
≠-3,故此图象不是③中的函数图象,故排除③.
对于④中的函数,当x= 时,y=-3sin π=0≠-3,故此图象不是④中的函数图象,故排除 ④.
时,y=-3sin π=0≠-3,故此图象不是④中的函数图象,故排除 ④.
故选:B.
点评:本题主要考查三角函数y=Asin(ωx+∅)的图象特征,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.
分析:由函数的图象知函数的周期为π,且函数在
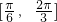 上是增函数,对于③中的函数,当x=
上是增函数,对于③中的函数,当x= 时,y=-3sin
时,y=-3sin ≠-3,对于④中的函数,当x=
≠-3,对于④中的函数,当x= 时,y=-3sin π=0≠-3,故排除③和④.
时,y=-3sin π=0≠-3,故排除③和④.解答:由函数的图象知函数的周期为π,且函数在
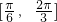 上是增函数.
上是增函数.由 2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,可得 kπ+
,可得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,故①中的函数在
,k∈z,故①中的函数在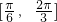 上是增函数.
上是增函数.由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得 kπ-
,可得 kπ- ≤x≤kπ-
≤x≤kπ- ,k∈z,故②中的函数在
,k∈z,故②中的函数在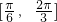 上是增函数.
上是增函数.综上,①②都满足这两个条件.
对于③中的函数,当x=
 时,y=-3sin
时,y=-3sin ≠-3,故此图象不是③中的函数图象,故排除③.
≠-3,故此图象不是③中的函数图象,故排除③.对于④中的函数,当x=
 时,y=-3sin π=0≠-3,故此图象不是④中的函数图象,故排除 ④.
时,y=-3sin π=0≠-3,故此图象不是④中的函数图象,故排除 ④.故选:B.
点评:本题主要考查三角函数y=Asin(ωx+∅)的图象特征,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
相关题目