题目内容
已知α,β,γ成等差数列,且公差为
,m为实常数,则sin2(α+m),sin2(β+m),sin2(γ+m)这三个三角函数式的算术平均数为
.
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:先利用倍角公式的变形把次数由二次降为一次,再利用和角公式、差角公式来统一角,达到化简求值的目的.
解答:解:由题意,α=β-
,γ=β+
,
∴sin2(α+m),sin2(β+m),sin2(γ+m)这三个三角函数式的算术平均数为S=
[sin2(α+m)+sin2(β+m)+sin2(γ+m)]=
[sin2(β-
+m)+sin2(β+m)+sin2(β+
+m)]=
[
+
+
]=
-
[cos(2β+2m-
)+cos(2β+2m+
)+cos(2β+2m)]=
-
[2cos(2β+2m)cos
+cos(2β+2m)]=
-
[2cos(2β+2m)(-
)+cos(2β+2m)]=
.
故答案为:
| 2π |
| 3 |
| 2π |
| 3 |
∴sin2(α+m),sin2(β+m),sin2(γ+m)这三个三角函数式的算术平均数为S=
| 1 |
| 3 |
| 1 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 3 |
1-cos(2β-
| ||
| 2 |
| 1-cos(2β+2m) |
| 2 |
1-cos(2β+
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 4π |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 4π |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题的综合性较高,对学生利用三角公式进行三角恒等变换的能力要求较高.对考点的发散思维点拨:新课标中的三角函数的考察要想推陈出新,可以不断改变考察方式和考察角度.引导、归纳及预测:虽然大纲中对三角函数的要求近年来有所降低,但对知识点的综合性却在提高,三角函数部分与其它章节的综合也在意料之中.解题方法技巧:本题的关键是三角函数式的化简,在化简时要及时调控变形方向,把握好“角的变化”、“函数名称的变化”、“运算形式的变化”这三种三角变换的时机.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
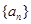 为等比数列, 其前
为等比数列, 其前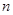 项和为
项和为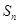 , 已知
, 已知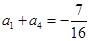 , 且对于任意的
, 且对于任意的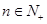 有
有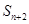 ,
, 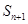 成等差;求数列
成等差;求数列