Question

【题目】已知椭圆的左，右焦点分别为，该椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线相切.

（I）求椭圆的方程；

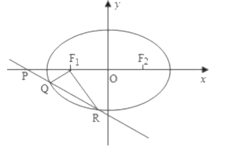
（Ⅱ）如图，若斜率为的直线与轴，椭圆顺次交于点在椭圆左顶点的左侧）且，求证：直线过定点；并求出斜率的取值范围.

Answer 1

【答案】（I）；（Ⅱ）证明见解析，.

【解析】

（I）根据椭圆离心率求得，根据圆心到直线的距离等于半径求得的值，进而求得的值和椭圆的标准方程.（II）设出两点的坐标，根据，得到，将两点坐标代入上式.设出直线的方程，代入椭圆方程并化简，写出韦达定理和判别式，将韦达定理得到的式子代入，化简后可求得直线所过定点.根据判别式，求得的取值范围.

（Ⅰ）解：椭圆的左，右焦点分别为，椭圆的离心率为，即有，即，，以原点为圆心，椭圆的短半轴长为半径的圆方程为，

直线与圆相切，则有，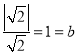

即有，

则椭圆C的方程为；

（Ⅱ）证明：设，

由，可得直线和关于x轴对称

即有，即，

即有，①

设直线，代入椭圆方程，可得，判别式，即为②，③，

代入①可得，，

将③代入，化简可得，

则直线的方程为，即．即有直线恒过定点．

将代入②，可得，

解得或

则直线的斜率的取值范围是．