题目内容
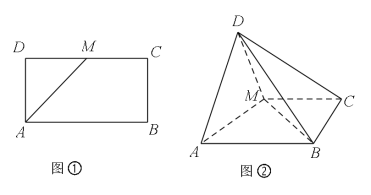
【题目】如图①,已知矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图②),并在图②中回答如下问题:
(如图②),并在图②中回答如下问题:
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据图①中数据可利用勾股定理逆定理得![]() ,再结合图②中平面
,再结合图②中平面![]() 平面
平面![]() ,利用面面垂直的性质定理可得
,利用面面垂直的性质定理可得![]() 平面
平面![]() ,从而证出
,从而证出![]() ;
;
(2)要求直线![]() 与平面
与平面![]() 所成角,只需求出直线
所成角,只需求出直线![]() 的方向向量
的方向向量![]() 与平面
与平面![]() 的法向量
的法向量![]() ,代入向量的夹角公式求出
,代入向量的夹角公式求出![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,利用
,利用![]() ,即可得到结果.
,即可得到结果.
(1)如图①,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
所以![]() ,所以
,所以![]() ,
,
由勾股定理逆定理得![]() ,
,
如图②,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)取![]() 的中点
的中点![]() ,作
,作![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,建立如图所示的空间直角坐标系,
,建立如图所示的空间直角坐标系,
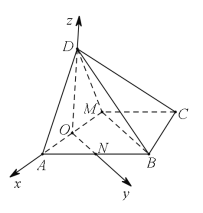
则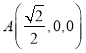 ,
,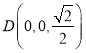 ,
,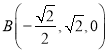 ,
,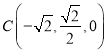 ,
,
所以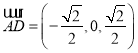 ,
,![]() ,
,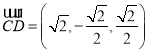 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由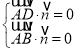 ,得
,得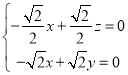 ,令
,令![]() ,则
,则![]() ,
,![]() .
.
所以![]() ,
,
所以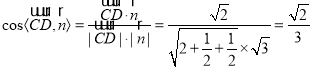 ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() ,
,
所以![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】某校高三年级有男生105人,女生126人,教师42人,用分层抽样的方法从中抽取13人进行问卷调查.设其中某项问题的选择只有“同意”,“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
同意 | 不同意 | 合计 | |
教师 | 1 | ||
女生 | 4 | ||
男生 | 2 |
(1)请完成此统计表;
(2)试估计高三年级学生“同意”的人数;
(3)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”、一人“不同意”的概率.