题目内容
在 中,
中, 分别为角
分别为角 所对的三边,
所对的三边, ,
,
(Ⅰ)求角 ;
;
(Ⅱ)若 ,角
,角 等于
等于 ,周长为
,周长为 ,求函数
,求函数 的取值范围.
的取值范围.
 中,
中, 分别为角
分别为角 所对的三边,
所对的三边, ,
,(Ⅰ)求角
 ;
;(Ⅱ)若
 ,角
,角 等于
等于 ,周长为
,周长为 ,求函数
,求函数 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)根据题目条件,容易联想到余弦定理,求出角
 ; (Ⅱ)求函数
; (Ⅱ)求函数 的取值范围,这是一个函数的值域问题,需先找出函数关系式,因此要先把各边长求出来,或用
的取值范围,这是一个函数的值域问题,需先找出函数关系式,因此要先把各边长求出来,或用 表示出来,方法是利用正弦定理来沟通三角形的边角关系,求出函数关系式后,不要忘记求函数的定义域,根据函数定义域去求函数的值域,这显然又是一个三角函数的值域问题,可化为
表示出来,方法是利用正弦定理来沟通三角形的边角关系,求出函数关系式后,不要忘记求函数的定义域,根据函数定义域去求函数的值域,这显然又是一个三角函数的值域问题,可化为 的类型求解.
的类型求解.试题解析:(Ⅰ)由
 ,得
,得 ,
, 3分
3分又
 ,
,  6分
6分(Ⅱ)


同理:
 9分
9分


故
 ,
, ,
, . 12分
. 12分
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的内角A、B、C所对的边为
的内角A、B、C所对的边为 ,
,  ,
,  ,且
,且 与
与 所成角为
所成角为 .
. 的取值范围.
的取值范围. 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,
, ,求a,c,的值.
,求a,c,的值. 中,角
中,角 的对边分别为
的对边分别为 ,
, 。
。 的值;(Ⅱ)求
的值;(Ⅱ)求 中,已知
中,已知 .
. 的值;
的值; ,
, ,求
,求 .
.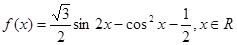
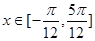 时,求函数
时,求函数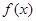 的最小值和最大值
的最小值和最大值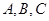 的对边分别为
的对边分别为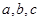 且
且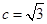 ,
,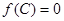 ,若
,若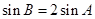 ,求
,求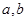 的值.
的值.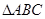 中,
中,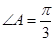 ,
,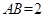 ,且
,且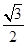 ,则边
,则边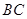 的长为_________.
的长为_________. 中,边
中,边 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,且满足
的对边,且满足 .
. ;
; ,
, ,求边
,求边 ,
, ,则A=
,则A=